题目内容
20. 某商场为促进消费,方便消费者停车,拟将商场门口某区域改建为停车场.如图,已知该区域边界处有台阶五级,每个台阶高150mm,宽300mm,现把台阶处改建为斜坡以方便汽车出入,为保证不损坏车的底盘,台阶下面设置缓坡带,使斜坡的倾斜角为5.711°,则台阶下面增加缓坡带的水平宽OA为多少m?(参考数据tan5.711°≈0.1000,sin5.711°≈0.09951,cos5.711°≈0.9950).
某商场为促进消费,方便消费者停车,拟将商场门口某区域改建为停车场.如图,已知该区域边界处有台阶五级,每个台阶高150mm,宽300mm,现把台阶处改建为斜坡以方便汽车出入,为保证不损坏车的底盘,台阶下面设置缓坡带,使斜坡的倾斜角为5.711°,则台阶下面增加缓坡带的水平宽OA为多少m?(参考数据tan5.711°≈0.1000,sin5.711°≈0.09951,cos5.711°≈0.9950).
分析 首先由题意可求得AB与BC的长,又由在Rt△BOC中,tan5.711°=$\frac{BC}{OB}$,即可求得OB的长,继而求得答案.
解答 解:由题意得:AB=5×300=1500(mm),BC=5×150=750(mm),
在Rt△BOC中,tan5.711°=$\frac{BC}{OB}$,
∴OB=$\frac{BC}{tan5.711°}$≈$\frac{750}{0.100}$=7500(mm),
∴OA=OB-AB=7500-1500=6000(mm)=6m.
∴台阶下面增加缓坡带的水平宽OA为6m.
点评 此题考查了坡度坡角问题.注意利用三角函数的知识求得OB的长是解此题的关键.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
5.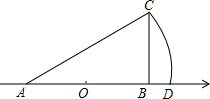 如图,数轴上点A表示的数是-1,原点O是线段AB的中点,∠BAC=30°,∠ABC=90°,以点A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数是( )
如图,数轴上点A表示的数是-1,原点O是线段AB的中点,∠BAC=30°,∠ABC=90°,以点A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数是( )
 如图,数轴上点A表示的数是-1,原点O是线段AB的中点,∠BAC=30°,∠ABC=90°,以点A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数是( )
如图,数轴上点A表示的数是-1,原点O是线段AB的中点,∠BAC=30°,∠ABC=90°,以点A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数是( )| A. | $\frac{2\sqrt{3}}{3}-1$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{3}}{3}-1$ |
9.下列说法正确的是( )
| A. | 所有的有理数都能用数轴上的点表示 | |
| B. | 符号不同的两个数互为相反数 | |
| C. | 有理数分为正数和负数 | |
| D. | 两数相加,和一定大于任何一个数 |



