题目内容
10.某商户销售甲、乙两种水果,根据以往经验和市场行情,预计:甲种水果每吨的销售利润m万元与销售量x吨之间部分对应值如下表:乙种水果每吨的销售利润为0.4万元.| x | … | 1 | 2 | 3 | 4 | 5 | … |
| m | … | 1.5 | 1.4 | 1.3 | 1.2 | 1.1 | … |
(2)两种水果的销售量与销售利润能否同时相等?如能,求出此时甲种水果的销售量;若不能,请说明理由;
(3)如果该商户预期销售甲,乙两种水果共16吨,试设计一种进货方案,使销售完这些水果后所获销售利润之和最大,并求出最大利润.
分析 (1)由表格数据可知甲种水果每吨的销售利润m(万元)与销售量x(吨)之间的函数关系式是一次函数,利用待定系数法求得答案即可;
(2)表示出乙种水果的销售利润与甲种水果的销售利润建立方程求得答案即可;
(3)设销售甲种水果x吨,则销售乙种水果16-x吨,求得销售利润之和,利用函数的性质求得最大利润即可.
解答 解:(1)设甲种水果每吨的销售利润m(万元)与销售量x(吨)之间的函数关系式m=kx+b,
把(1,1.5),(2,1.4)代入得$\left\{\begin{array}{l}{k+b=1.5}\\{2k+b=1.4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-0.1}\\{b=1.6}\end{array}\right.$.
∴m=-0.1x+1.6,
∴甲种水果的销售利润y=mx=(-0.1x+1.6)x=-0.1x2+1.6x,
因此甲种水果的销售利润y(万元)与销售量x(吨)之间的函数关系式y=-0.1x2+1.6x;
(2)乙种水果的销售利润y=0.4x,
由题意得0.4x=-0.1x2+1.6x
解得:x=12或0(舍去),
所以两种水果的销售量与销售利润能同时相等,此时甲种水果的销售量为12吨;
(3)设销售甲种水果x吨,则销售乙种水果16-x吨,由题意得
总销售利润y=-0.1x2+1.6x+0.4(16-x)=-0.1x2+1.2x+6.4,(0≤x≤16)
∵a=-0.1<0,
∴抛物线开口向下,
∵x=-$\frac{b}{2a}$=$\frac{1.2}{2×0.1}$=6,
∴当x=6时,ymax=-0.1×36+1.2×6+6.4=10(万元),
∴当x=6时,函数最大值是10,
即销售甲种水果6吨,销售乙种水果10吨,销售利润最大为10万元.
点评 此题考查一次函数的实际运用,待定系数法求函数解析式,掌握待定系数法求函数解析式以及函数的性质是解决问题的关键.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案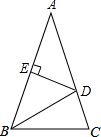 如图,在△ABC中,AB=AC,AB的垂直平分线DE交AB于点E,交AC于点D,△ABC,△DBC的周长分别是60和38,求AC,BC的长.
如图,在△ABC中,AB=AC,AB的垂直平分线DE交AB于点E,交AC于点D,△ABC,△DBC的周长分别是60和38,求AC,BC的长.