题目内容
7.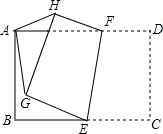 如图,在矩形ABCD中,AB=4,BC=6,点E是BC的中点,点F在AD上运动,沿直线EF折叠四边形CDFE,得到四边形GHFE,其中点C落在点G处,连接AG,AH,则AG的最小值是2.
如图,在矩形ABCD中,AB=4,BC=6,点E是BC的中点,点F在AD上运动,沿直线EF折叠四边形CDFE,得到四边形GHFE,其中点C落在点G处,连接AG,AH,则AG的最小值是2.
分析 如图,连接AE,当A、G、E共线时,AG最小,先求出AE,根据AG′=AE-EG′即可解决问题.
解答 解:如图 ,连接AE.
,连接AE.
∵四边形ABCD是矩形,
∴∠B=90°,BE=EC=3,AB=4,
∴AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5.
当A、G、E共线时,AG最小,
此时AG′=AE-EG′=5-3=2.
故答案为2.
点评 本题考查矩形的性质、翻折变换、勾股定理等知识,解题的关键是利用两点之间线段最短解决问题,属于中考常考题型.

练习册系列答案
相关题目
18.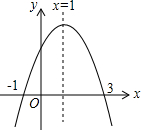 如图为二次函数y=ax2+bx+c的图象,给出下列说法:①abc>0;②方程ax2+bx+c=0的根为x1=-1,x2=3;③6a-b+c<0;④a-am2>bm-b,且m-1≠0,其中正确的说法有( )
如图为二次函数y=ax2+bx+c的图象,给出下列说法:①abc>0;②方程ax2+bx+c=0的根为x1=-1,x2=3;③6a-b+c<0;④a-am2>bm-b,且m-1≠0,其中正确的说法有( )
 如图为二次函数y=ax2+bx+c的图象,给出下列说法:①abc>0;②方程ax2+bx+c=0的根为x1=-1,x2=3;③6a-b+c<0;④a-am2>bm-b,且m-1≠0,其中正确的说法有( )
如图为二次函数y=ax2+bx+c的图象,给出下列说法:①abc>0;②方程ax2+bx+c=0的根为x1=-1,x2=3;③6a-b+c<0;④a-am2>bm-b,且m-1≠0,其中正确的说法有( )| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ②④ |
12.关于x的分式方程$\frac{m}{x+5}=1$,下列说法正确的是( )
| A. | 方程的解是x=m-5 | B. | m>5时,方程的解是正数 | ||
| C. | m<5时,方程的解为负数 | D. | 无法确定 |
16.下列四组线段中,可以构成直角三角形的是( )
| A. | 1,$\sqrt{2}$,3 | B. | 1.5,2.5,3 | C. | 4,5,6 | D. | 6,8,10 |
 如图,李明在一块平地上测山高,现在B出测得山顶A的仰角为30°,然后再向山脚直行100米到达C处,再测得山顶A的仰角为60°,那么山高AD为50$\sqrt{3}$米.
如图,李明在一块平地上测山高,现在B出测得山顶A的仰角为30°,然后再向山脚直行100米到达C处,再测得山顶A的仰角为60°,那么山高AD为50$\sqrt{3}$米. 如图,在平面直角坐标系中,一个正方形的中点原点O,且一组对边与y轴平行,点A(a,-4a)是反比例函数y=$\frac{k}{x}$的图象上与正方形的一个交点,若图中阴影部分的面积等于16,则k的值为( )
如图,在平面直角坐标系中,一个正方形的中点原点O,且一组对边与y轴平行,点A(a,-4a)是反比例函数y=$\frac{k}{x}$的图象上与正方形的一个交点,若图中阴影部分的面积等于16,则k的值为( )