题目内容
15. 如图,李明在一块平地上测山高,现在B出测得山顶A的仰角为30°,然后再向山脚直行100米到达C处,再测得山顶A的仰角为60°,那么山高AD为50$\sqrt{3}$米.
如图,李明在一块平地上测山高,现在B出测得山顶A的仰角为30°,然后再向山脚直行100米到达C处,再测得山顶A的仰角为60°,那么山高AD为50$\sqrt{3}$米.
分析 根据仰角和俯角的定义得到∠ABD=30°,∠ACD=60°,设AD=xm,先在Rt△ACD中,利用∠ACD的正切可得CD=$\frac{\sqrt{3}}{3}$x,则BD=BC+CD=$\frac{\sqrt{3}}{3}$x+100,然后在Rt△ABD中,利用∠ABD的正切得到AD的值.
解答 解:∵∠ABD=30°,∠ACD=60°,BC=100m,
设AD=xm,
在Rt△ACD中,∵tan∠ACD=$\frac{AD}{CD}$=$\sqrt{3}$,
∴CD=$\frac{\sqrt{3}}{3}$x,
∴BD=BC+CD=$\frac{\sqrt{3}}{3}$x+100,
在Rt△ABD中,∵tan∠ABD=$\frac{AD}{BD}$,
∴x=50$\sqrt{3}$米.
故答案为:50$\sqrt{3}$.
点评 本题考查了解直角三角形-的应用-仰角俯角:解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,要善于读懂题意,把实际问题划归为直角三角形中边角关系问题加以解决.

练习册系列答案
相关题目
5.下列调查中,适宜采用全面调查(普查)方式的是( )
| A. | 对我市中学生心理健康状况的调差 | |
| B. | 调差我市冷饮市场雪糕质量情况 | |
| C. | 调差我国网民对某件事的看法 | |
| D. | 对我国首架大型民用飞机各零部件质量的检查 |
6.深圳今年4月份某星期的最高气温如下(单位℃):26,25,27,28,27,25,25,则这个星期的最高气温的众数和中位数分别是( )
| A. | 25,26 | B. | 25,26.5 | C. | 27,26 | D. | 25,28 |
3.若方程组$\left\{{\begin{array}{l}{3x+5y=a+4}\\{2x+3y=a}\end{array}}\right.$的解x与y的和为3,则ax的值是( )
| A. | -42 | B. | 0 | C. | 7 | D. | 14 |
10.某校举办校园文化艺术节,在这次艺术节上,合唱比赛设置了6个获奖名额,共有11个代表队参加,他们的比赛得分均不相同,若知道某个代表队的得分,要判断他们是否获奖,在下列11个代表队成绩的统计量中,只需知道( )
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
20.如果∠1=∠2,∠1+∠3=90°,∠2+∠4=90°,那么∠3与∠4的关系是( )
| A. | 互余 | B. | 相等 | C. | 互补 | D. | 以上都不对 |
4. 如图,直线a,b分别与c相交,在标出的角∠2,∠3,∠4,∠5中,与∠1是同位角的是( )
如图,直线a,b分别与c相交,在标出的角∠2,∠3,∠4,∠5中,与∠1是同位角的是( )
 如图,直线a,b分别与c相交,在标出的角∠2,∠3,∠4,∠5中,与∠1是同位角的是( )
如图,直线a,b分别与c相交,在标出的角∠2,∠3,∠4,∠5中,与∠1是同位角的是( )| A. | ∠2 | B. | ∠3 | C. | ∠4 | D. | ∠5 |
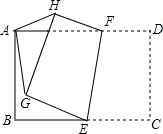 如图,在矩形ABCD中,AB=4,BC=6,点E是BC的中点,点F在AD上运动,沿直线EF折叠四边形CDFE,得到四边形GHFE,其中点C落在点G处,连接AG,AH,则AG的最小值是2.
如图,在矩形ABCD中,AB=4,BC=6,点E是BC的中点,点F在AD上运动,沿直线EF折叠四边形CDFE,得到四边形GHFE,其中点C落在点G处,连接AG,AH,则AG的最小值是2.