题目内容
18.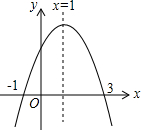 如图为二次函数y=ax2+bx+c的图象,给出下列说法:①abc>0;②方程ax2+bx+c=0的根为x1=-1,x2=3;③6a-b+c<0;④a-am2>bm-b,且m-1≠0,其中正确的说法有( )
如图为二次函数y=ax2+bx+c的图象,给出下列说法:①abc>0;②方程ax2+bx+c=0的根为x1=-1,x2=3;③6a-b+c<0;④a-am2>bm-b,且m-1≠0,其中正确的说法有( )| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ②④ |
分析 ①由抛物线的开口向下,对称轴在y轴的右侧,判断a,b与0的关系,得到abc<0;故①错误;
②由抛物线与x轴的交点坐标得到方程ax2+bx+c=0的根为x1=-1,x2=3;故②正确;
③由a<0,x=-1时,得到-5a>0,y=a+b+c=0,得到a-b+c<-5a,故③正确;
④由抛物线的顶点横坐标为1,且开口向下,得到当x=1时,对应的函数值最大,即a+b+c>am2+bm+c(m-1≠0),得到a+b>am2+bm,故④正确.
解答 解:∵抛物线的开口方向向下,
∴a<0,
∵对称轴在y轴的右边,
∴b>0,
∵抛物线与y轴的交点在x轴的上方,
∴c>0,
∴abc<0,故①错误;
根据图象知道抛物线与x轴的交点的横坐标分别为x=-1或x=3,
∴方程ax2+bx+c=0的根为x1=-1、x2=3,故②正确;
③∵a<0,∴-5a>0
当x=-1时,a-b+c=0,
∴a-b+c<-5a,
∴6a-b+c<0;故③正确;
④∵抛物线的顶点横坐标为1,且开口向下,
∴当x=1时,对应的函数值最大,即a+b+c>am2+bm+c(m-1≠0),
∴a+b>am2+bm,
∴a-am2>bm-b,本④正确;
故选B.
点评 本题主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
相关题目
8.景新中学为了了解学生体育中考备考情况,随机抽查了10名学生的引体向上,结果如下表:
则关于这10名学生的引体向上数据,下列说法错误的是( )
| 引体向上(次) | 18 | 19 | 20 |
| 学生数 | 2 | 6 | 2 |
| A. | 极差是2 | B. | 众数是19 | C. | 平均数是19 | D. | 方差是4 |
9.下列各式运算结果为a5的是( )
| A. | (a2)3 | B. | a2+a3 | C. | a2•a3 | D. | a10÷a2 |
6.深圳今年4月份某星期的最高气温如下(单位℃):26,25,27,28,27,25,25,则这个星期的最高气温的众数和中位数分别是( )
| A. | 25,26 | B. | 25,26.5 | C. | 27,26 | D. | 25,28 |
3.若方程组$\left\{{\begin{array}{l}{3x+5y=a+4}\\{2x+3y=a}\end{array}}\right.$的解x与y的和为3,则ax的值是( )
| A. | -42 | B. | 0 | C. | 7 | D. | 14 |
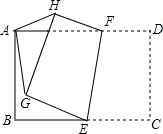 如图,在矩形ABCD中,AB=4,BC=6,点E是BC的中点,点F在AD上运动,沿直线EF折叠四边形CDFE,得到四边形GHFE,其中点C落在点G处,连接AG,AH,则AG的最小值是2.
如图,在矩形ABCD中,AB=4,BC=6,点E是BC的中点,点F在AD上运动,沿直线EF折叠四边形CDFE,得到四边形GHFE,其中点C落在点G处,连接AG,AH,则AG的最小值是2.