题目内容
19.某宾馆有客房100间,当每一间一天的定价为180元时,客房会全部租出.当定价每增加10元时,就会有5间客房空着.(1)若某日的定价增加了20元,则这天该宾馆客房的收入为18000元.
(2)若某日宾馆客房的收入为17600元,试求这天每间客房的定价.
(3)求定价x为多少元时,客房收入y最高.
分析 (1)由于客房100间供游客居住,当每间客房的定价为每天180元时,客房恰好全部租出;如果每间客房每天的定价每增加10元,就会减少5间客房出租,如果每间客房天天的定价增加了20元,宾馆的出租的客房为100-5×2=90间,根据利润=客房数×房价,求得收入即可;
(2)设这天每间客房的定价为x元,利用利润=客房数×房价列方程即可求解;
(3)由利润=客房数×房价,利用这个等式即可列出函数,利用函数的性质求得最大值即可.
解答 解:(1)(180+20)×(100-5×20÷10)=18000(元).
答:这天该宾馆客房的收入为18000元.
(2)设这天每间客房的定价为x元,由题意得
x(100-$\frac{x-180}{10}$×5)=17600,
解得:x1=160,x2=220,
当x=220时,100-$\frac{x-180}{10}$×5=0,不合题意,舍去.
答:这天每间客房的定价为160元;
(3)由题意得y=x(100-$\frac{x-180}{10}$×5)=-$\frac{1}{2}$(x-190)+18050,
当定价x为190元时,客房收入y最高为18050元.
点评 此题考查二次函数的实际运用,一元二次方程的实际运用,掌握销售问题中的基本数量关系是解决问题的关键.

练习册系列答案
相关题目
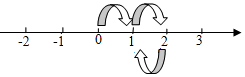
9.如图,数轴上有一个质点从原点出发,沿数轴跳动,每次向正方向或负方向跳1个单位,经过5次跳动,质点落在表示数3的点上(允许重复过此点),则质点的不同运动方案共有( )

| A. | 2种 | B. | 3种 | C. | 4种 | D. | 5种 |
14.点A(-4,y1),B(2,y2)都在直线y=-x-1上,则y1与y2的大小关系为( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 无法确定 |
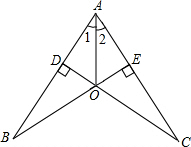 如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD交于点O,OB=OC.求证:∠1=∠2.
如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD交于点O,OB=OC.求证:∠1=∠2.