题目内容
8.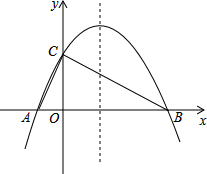 如图,已知抛物线y=-$\frac{1}{4}$x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(-2,0).
如图,已知抛物线y=-$\frac{1}{4}$x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(-2,0).(1)求抛物线的解析式及它的对称轴方程;
(2)求点C的坐标,连接AC、BC并求线段BC所在直线的解析式;
(3)试判断△AOC与△COB是否相似?并说明理由.
分析 (1)把A点坐标代入抛物线解析式可求得b的值,则可求得抛物线解析式及其对称轴方程;
(2)由抛物线解析式可求得A、B、C的坐标,根据待定系数法可求得直线BC的解析式;
(3)由A、B、C的坐标可求得OA、OC、OB的长,根据相似三角形的判定可证明△AOC∽△COB.
解答 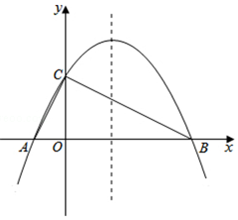 解:
解:
(1)∵抛物线y=-$\frac{1}{4}$x2+bx+4的图象经过点A(-2,0),
∴-$\frac{1}{4}$×(-2)2+b×(-2)+4=0,解得b=$\frac{3}{2}$,
∴抛物线解析式为 y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4,
又∵y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4=-$\frac{1}{4}$(x-3)2+$\frac{25}{4}$,
∴对称轴方程为x=3;
(2)在y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4中,令x=0,得y=4,
∴C(0,4),
令y=0,即-$\frac{1}{4}$x2+$\frac{3}{2}$x+4=0,整理得x2-6x-16=0,解得x=8或x=-2,
∴A(-2,0),B(8,0),
设直线BC的解析式为y=kx+b,
把B(8,0),C(0,4)的坐标分别代入解析式$\left\{\begin{array}{l}{8k+b=0}\\{b=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=4}\end{array}\right.$,
∴直线BC的解析式为y=-$\frac{1}{2}$x+4;
(3)△AOC∽△COB成立.
理由如下:
在△AOC与△COD中,
∵OA=2,OC=4,OB=8,
∴$\frac{OA}{OC}$=$\frac{OC}{OB}$,
又∵∠AOC=∠BOC=90°,
∴△AOC∽△COB.
点评 本题为一次函数的综合应用,涉及待定系数法、二次函数的性质、一元二次方程及相似三角形的判定等知识.在(1)中掌握函数图象上的点的坐标满足函数解析式是解题的关键,在(2)中求得B、C的坐标是解题的关键,在(3)中分别求得OA、OC、OB的长是解题的关键.本题考查知识点较多,综合性较强,但难度不大.

| 组别 | 成绩(分) | 频数(人数) | 频率 |
| 第1组 | 5 | 4 | a |
| 第2组 | 6 | 5 | 0.125 |
| 第3组 | 7 | b | 0.15 |
| 第4组 | 8 | 12 | 0.25 |
| 第5组 | 9 | 8 | 0.2 |
| 第6组 | 10 | 5 | 0.125 |
(2)统计表后三行中哪一个数据是错误的?该数据的正确值是多少?
(3)求这些学生成绩的中位数和众数.
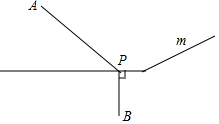 如图所示,在两个村庄A,B附近的河流可以近似地看成一条折线段(图中m)A,B分别在河的两旁,现要在河边修一个水泵站,同时向A,B两村供水,为了节约建设的费用,就要使所铺设的管道最短,某人甲提出了这样的建议:从点B向河道作垂线交m于点P,则点P为水泵站的位置.
如图所示,在两个村庄A,B附近的河流可以近似地看成一条折线段(图中m)A,B分别在河的两旁,现要在河边修一个水泵站,同时向A,B两村供水,为了节约建设的费用,就要使所铺设的管道最短,某人甲提出了这样的建议:从点B向河道作垂线交m于点P,则点P为水泵站的位置.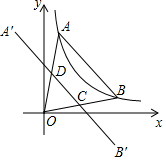 如图,点A、B在函数y=$\frac{1}{x}$(x>0)的图象上,点A在点B的左侧,且OA=OB,点A关于y轴的对称点为A′,点B关于x轴的对称点为B′,连接A′B′分别交OA、OB于点D、C.若四边形ABCD的面积为$\frac{6}{5}$,则点A的坐标为($\frac{1}{2}$,2),点C的坐标为($\frac{6}{5}$,$\frac{3}{10}$).
如图,点A、B在函数y=$\frac{1}{x}$(x>0)的图象上,点A在点B的左侧,且OA=OB,点A关于y轴的对称点为A′,点B关于x轴的对称点为B′,连接A′B′分别交OA、OB于点D、C.若四边形ABCD的面积为$\frac{6}{5}$,则点A的坐标为($\frac{1}{2}$,2),点C的坐标为($\frac{6}{5}$,$\frac{3}{10}$).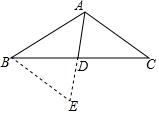 如图,在△ABC中,AD为BC边上中线.若AB=5,AC=7,则AD的取值范围1<AD<6.
如图,在△ABC中,AD为BC边上中线.若AB=5,AC=7,则AD的取值范围1<AD<6.