题目内容
4.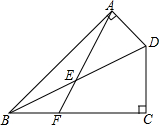 如图,在四边形ABCD中,∠BAD=∠BCD=90°,∠ABC=45°,点E为BD边中点,AE交BC于F.若BF=3,CF=5,则AD的长为2$\sqrt{2}$.
如图,在四边形ABCD中,∠BAD=∠BCD=90°,∠ABC=45°,点E为BD边中点,AE交BC于F.若BF=3,CF=5,则AD的长为2$\sqrt{2}$.
分析 如图,作DS∥BC交AF于S,作AH⊥BC于H,延长AD,BC交于G,于是得到∠SDE=∠FBE,根据等腰直角三角形的性质得到CD=CG,设CD=x,则CG=x,DG=$\sqrt{2}$x,BG=8+x,根据全等三角形的判定和性质得到SD=BF=3,根据平行线分线段成比例定理得到HG=6,于是得到结论.
解答 解: 如图,作DS∥BC交AF于S,作AH⊥BC于H,延长AD,BC交于G,
如图,作DS∥BC交AF于S,作AH⊥BC于H,延长AD,BC交于G,
∴∠SDE=∠FBE,
∵∠ABC=45°,
∴∠BAH=45°,
∴∠GAH=45°,
∴∠G=45°,
∵∠BCD=90°,
∴∠CDG=45°,
∴CD=CG,
设CD=x,则CG=x,DG=$\sqrt{2}$x,BG=8+x,
∴FG=x+5,
∴HG=AG=$\frac{8+x}{2}$,CH=$\frac{8+x}{2}$-x=$\frac{8-x}{2}$,
在△SED与△FEB中,$\left\{\begin{array}{l}{∠SDE=∠FBE}\\{EB=ED}\\{∠SED=∠FEB}\end{array}\right.$,
∴△SED≌△FEB,
∴SD=BF=3,
∵SD∥BC,DC∥AH,
∴$\frac{SD}{FG}$=$\frac{AD}{AG}$=$\frac{CH}{HG}$,
$\frac{3}{5+x}$=$\frac{\frac{8-x}{2}}{\frac{8+x}{2}}$,
∴x2=16,
∴x=4,
∴HG=6,
∴AG=6$\sqrt{2}$,
∴AD=6$\sqrt{2}$-4$\sqrt{2}$=2$\sqrt{2}$,
故答案为:2$\sqrt{2}$.
点评 本题考查了直角三角形斜边上的中线,全等三角形的判定和性质,平行线分线段成比例定理,正确的作出辅助线是解题的关键.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| A. | 合理的 | B. | 不能确定 | C. | 不合理的 | D. | 以上都不对 |
| A. | $\frac{7}{40}$ | B. | $\frac{1}{24}$ | C. | $\frac{4}{15}$ | D. | $\frac{5}{12}$ |
 已知抛物线y=a(x+1)2+k交x轴于A、B两点(点A在点B左侧),AB=4,顶点E在x轴上方,tan∠EAB=2.
已知抛物线y=a(x+1)2+k交x轴于A、B两点(点A在点B左侧),AB=4,顶点E在x轴上方,tan∠EAB=2.
 如图,已知一把展开的扇子的圆心角是150°,扇子的骨架AO的长是40厘米,扇面宽AB的长是30厘米,求扇面的面积.(结果保留π)
如图,已知一把展开的扇子的圆心角是150°,扇子的骨架AO的长是40厘米,扇面宽AB的长是30厘米,求扇面的面积.(结果保留π)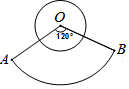 如图,已知圆O的周长与扇形OAB所对的弧长的比值为1,那么圆O的面积与扇形OAB的面积的比值为$\frac{1}{3}$.
如图,已知圆O的周长与扇形OAB所对的弧长的比值为1,那么圆O的面积与扇形OAB的面积的比值为$\frac{1}{3}$.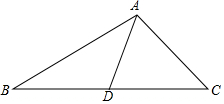 如图,在三角形ABC中,AD为中线,AB=4,AC=2,AD为整数,求AD的长.
如图,在三角形ABC中,AD为中线,AB=4,AC=2,AD为整数,求AD的长.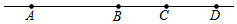 如图,一条直线上有四点A、B、C、D,以下说法:①图中共有6条线段;②若B为AD的中点,则$\frac{BC}{CA-CD}$=$\frac{1}{2}$;③若想在直线上找一点,使这个点到A、B、C、D四个点的距离之和最小,则这个点一定在线段BC上,其中正确的有①③.
如图,一条直线上有四点A、B、C、D,以下说法:①图中共有6条线段;②若B为AD的中点,则$\frac{BC}{CA-CD}$=$\frac{1}{2}$;③若想在直线上找一点,使这个点到A、B、C、D四个点的距离之和最小,则这个点一定在线段BC上,其中正确的有①③.