题目内容
19.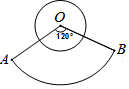 如图,已知圆O的周长与扇形OAB所对的弧长的比值为1,那么圆O的面积与扇形OAB的面积的比值为$\frac{1}{3}$.
如图,已知圆O的周长与扇形OAB所对的弧长的比值为1,那么圆O的面积与扇形OAB的面积的比值为$\frac{1}{3}$.
分析 设圆O的半径为r,则圆O的周长为2πr,设扇形OAB所在的半径为R,则扇形OAB的弧长为$\frac{120}{360}$×πR×2=$\frac{2}{3}$πR,由已知得2πr:$\frac{2}{3}$πR=1,求出r与R的关系,再根据圆面积公式解答即可.
解答 解:设圆O的半径为r,则圆O的周长为2πr,
设扇形OAB所在的半径为R,则扇形OAB的弧长为$\frac{120}{360}$×πR×2=$\frac{2}{3}$πR,
(2πr):($\frac{2}{3}$×πR×2)=1,
∴2πr=$\frac{2}{3}$πR,
∴r=$\frac{1}{3}$R,
即R=3r
∴(πr2):($\frac{120}{360}$πR2)
=πr2:[$\frac{1}{3}$π(3r)2]
=πr2:[$\frac{1}{3}$π×9r2]
=πr2:[3πr2]
=1:3
=$\frac{1}{3}$
即:圆O的面积与扇形OAB的面积的比值为$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 解答本题的关键是先求出圆O与扇形OAB的半径之间的关系,然后利用圆面积公式进一步解答即可.

练习册系列答案
相关题目
18. 如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )
如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )
 如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )
如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )| A. | 四边形ACDF是平行四边形 | |
| B. | 当点E为BC中点时,四边形ACDF是矩形 | |
| C. | 当点B与点E重合时,四边形ACDF是菱形 | |
| D. | 四边形ACDF不可能是正方形 |
14.在下列分数中:不能化成有限小数的是( )
| A. | $\frac{4}{25}$ | B. | $\frac{9}{16}$ | C. | $\frac{3}{12}$ | D. | $\frac{1}{30}$ |
9. 如图所示为打碎的一块三角形玻璃,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( )
如图所示为打碎的一块三角形玻璃,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( )
 如图所示为打碎的一块三角形玻璃,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( )
如图所示为打碎的一块三角形玻璃,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( )| A. | 带①去 | B. | 带②去 | C. | 带③去 | D. | 带①和②去 |
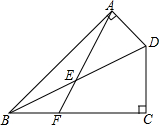 如图,在四边形ABCD中,∠BAD=∠BCD=90°,∠ABC=45°,点E为BD边中点,AE交BC于F.若BF=3,CF=5,则AD的长为2$\sqrt{2}$.
如图,在四边形ABCD中,∠BAD=∠BCD=90°,∠ABC=45°,点E为BD边中点,AE交BC于F.若BF=3,CF=5,则AD的长为2$\sqrt{2}$.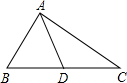 如图,在△ABC中,AD是BC边上的中线,若AB=3cm,AC=5cm,则AD的取值范围是1cm<AD<4cm.
如图,在△ABC中,AD是BC边上的中线,若AB=3cm,AC=5cm,则AD的取值范围是1cm<AD<4cm.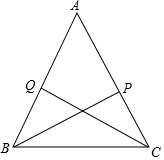 如图,CQ和BP是△ABC的角平分线,且BQ=CP,求证:AB=AC.
如图,CQ和BP是△ABC的角平分线,且BQ=CP,求证:AB=AC.