题目内容
13.下列分数中,能化成有限小数是( )| A. | $\frac{7}{40}$ | B. | $\frac{1}{24}$ | C. | $\frac{4}{15}$ | D. | $\frac{5}{12}$ |
分析 首先,要把分数化成最简分数,再根据一个最简分数,如果分母中除了2与5以外,不能含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数.
解答 解:$\frac{1}{24}$的分母中含有质因数3,所以不能化成有限小数;
$\frac{7}{40}$分母中只含有质因数2和5,所以能化成有限小数;
$\frac{4}{15}$的分母中含有质因数3,所以不能化成有限小数;
$\frac{5}{12}$的分母中含有质因数3,所以不能化成有限小数;
答:能化成有限小数的是$\frac{7}{40}$.
故选:A.
点评 此题考查的目的是理解掌握判断一个分数能否化成有限小数的方法.

练习册系列答案
相关题目
18.已知2x=y,m是任意一个有理数,下列式子不一定成立的是( )
| A. | 2x-m=y-m | B. | 2mx=my | C. | 2x+$\frac{m}{4}$=y+$\frac{m}{4}$ | D. | $\frac{2x}{m-3}$=$\frac{y}{m-3}$ |
2.一个三角形的三边长分别为4,7,x,那么x可能的值是( )
| A. | 3 | B. | 7 | C. | 11 | D. | 15 |
3. 如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;
如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;
将C1绕点A1旋转180°得C2,交x轴于点A2;
将C2绕点A2旋转180°得C3,交x轴于点A3;
…
如此进行下去,直至得C13.则C13的顶点坐标为( )
 如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;
如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;
将C2绕点A2旋转180°得C3,交x轴于点A3;
…
如此进行下去,直至得C13.则C13的顶点坐标为( )
| A. | ($\frac{69}{2}$,$\frac{9}{4}$) | B. | ($\frac{69}{2}$,-$\frac{9}{4}$) | C. | ($\frac{75}{2}$,$\frac{9}{4}$) | D. | ($\frac{75}{2}$,-$\frac{9}{4}$) |
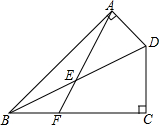 如图,在四边形ABCD中,∠BAD=∠BCD=90°,∠ABC=45°,点E为BD边中点,AE交BC于F.若BF=3,CF=5,则AD的长为2$\sqrt{2}$.
如图,在四边形ABCD中,∠BAD=∠BCD=90°,∠ABC=45°,点E为BD边中点,AE交BC于F.若BF=3,CF=5,则AD的长为2$\sqrt{2}$.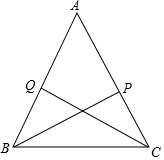 如图,CQ和BP是△ABC的角平分线,且BQ=CP,求证:AB=AC.
如图,CQ和BP是△ABC的角平分线,且BQ=CP,求证:AB=AC.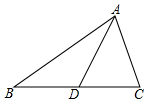 如图,△ABC中,AD是中线,AC=3,AB=5,则AD的取值范围是1<AD<4.
如图,△ABC中,AD是中线,AC=3,AB=5,则AD的取值范围是1<AD<4.