题目内容
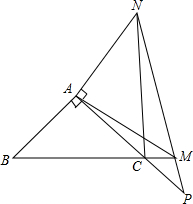 如图,△ABC中,AB=AC,∠B=45°,M是BC延长线上一点,△AMN∽△ABC,MN交AC延长线于点P,连接CN.
如图,△ABC中,AB=AC,∠B=45°,M是BC延长线上一点,△AMN∽△ABC,MN交AC延长线于点P,连接CN.(1)请尽可能多找出图中的相似三角形(题中给出的除外);
(2)你能找到CM、CN与CA的数量关系吗?并说明理由.
考点:相似三角形的判定与性质
专题:常规题型
分析:(1)先证明△ABM和△ACN,找出相等角即可解题;
(2)易证CN=BM,BC=
CA,即可求得CM、CN与CA的数量关系.
(2)易证CN=BM,BC=
| 2 |
解答:解:(1)如图,

∵△AMN∽△ABC,AB=AC,∴AM=AN,
∵∠BAM=∠BAC+∠CAM,∠CAN=∠CAM+∠MAN,
∴∠BAM=∠CAN,
在△ABM和△ACN中,
,
∴△ABM≌△ACN(SAS),
∴∠ANC=∠AMB,∠NCA=∠B=45°,
∴∠CAM=∠CNM,
∴△ACM∽△AMP∽△NCP,
∴△ACQ∽△NMQ,
∴△ANQ∽△CMQ,
∴△ANP∽△CMP,
(2)∵△ABM≌△ACN,
∴CN=BM,
∵AB=AC,∠BAC=90°,∴BC=
CA,
∴CN=BM=BC+CM=
CA+CM,
∴CN=
CA+CM.

∵△AMN∽△ABC,AB=AC,∴AM=AN,
∵∠BAM=∠BAC+∠CAM,∠CAN=∠CAM+∠MAN,
∴∠BAM=∠CAN,
在△ABM和△ACN中,
|
∴△ABM≌△ACN(SAS),
∴∠ANC=∠AMB,∠NCA=∠B=45°,
∴∠CAM=∠CNM,
∴△ACM∽△AMP∽△NCP,
∴△ACQ∽△NMQ,
∴△ANQ∽△CMQ,
∴△ANP∽△CMP,
(2)∵△ABM≌△ACN,
∴CN=BM,
∵AB=AC,∠BAC=90°,∴BC=
| 2 |
∴CN=BM=BC+CM=
| 2 |
∴CN=
| 2 |
点评:本题考查了全等三角形的判定和全等三角形对应角、对应边相等的性质,考查了相似三角形的判定和相似三角形对应角相等的性质.

练习册系列答案
相关题目
 如图,AB=AC=12,BC=7,∠A=40°,AB的垂直平分线交AB于点交于点D,交AC于点E,△BCE的周长是
如图,AB=AC=12,BC=7,∠A=40°,AB的垂直平分线交AB于点交于点D,交AC于点E,△BCE的周长是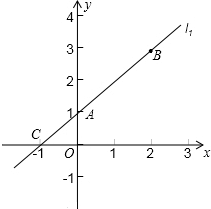 如图,已知直线l1经过点A(0,1)与点B(2,3),另一条直线l2经过点B,且与x轴相交于点P(m,0).
如图,已知直线l1经过点A(0,1)与点B(2,3),另一条直线l2经过点B,且与x轴相交于点P(m,0).