题目内容
已知a,b,c为三角形的三边,若a=2,b=3,当c为何值时,△ABC是:
(1)锐角三角形?
(2)直角三角形?
(3)钝角三角形?
(1)锐角三角形?
(2)直角三角形?
(3)钝角三角形?
考点:勾股定理的逆定理
专题:
分析:分三种情况讨论:①a<b<c,②a<c<b,③c<a<b,(1)①a2+b2>c2,②a2+c2>b2,③c2+a2>b2;(2)①a2+b2=c2,②a2+c2=b2,③c2+a2=b2;(3)①a2+b2<c2,②a2+c2<b2,③c2+a2<b2.然后即可求出c的范围.
解答:解:(1)分三种情况讨论:①a<b<c,②a<c<b,③c<a<b,
①a<b<c,
当a2+b2>c2时,△ABC是锐角三角形,
即c2<22+32=13,
∴c<
,
∵a<b<c
∴3<c<
.
∴当3<c<
时,△ABC是锐角三角形,
②a<c<b
当a2+c2>b2时,△ABC是锐角三角形,
即c2>b2-a2=32-22=5,
∴c>
,
∵a<c<b,
∴
<c<3,
∴当
<c<3,时,△ABC是锐角三角形,
③c<a<b
当c2+a2>b2时,△ABC是锐角三角形,
即c2>b2-a2=32-22=5,
∴c>
,
∵c<a<b,
∴
<c<2(舍去),
∴当
<c<3,或3<c<
时,△ABC是锐角三角形;
(2)分三种情况讨论:①a<b<c,②a<c<b,③c<a<b,
①a<b<c
当a2+b2=c2时,△ABC是直角三角形,
即c2=22+32=13,
∴c=
,
∴当c=
时,△ABC是直角三角形,
②a<c<b
当a2+c2=b2时,△ABC是直角三角形,
即c2=b2-a2=32-22=5,
∴c=
,
∴当c=
时,△ABC是直角三角形,
③c<a<b
当c2+a2=b2时,△ABC是直角三角形,
即c2=b2-a2=32-22=5,
∴c=
,
∴当c=
时,△ABC是直角三角形,
∴当c=
或
时,△ABC是直角三角形;
(3)分三种情况讨论:①a<b<c,②a<c<b,③c<a<b,
①a<b<c,
当a2+b2<c2时,△ABC是钝角三角形,
即c2>22+32=13,
∴c>
,
∵a<b<c
∴c>
.
∴当c>
时,△ABC是钝角三角形,
②a<c<b
当a2+c2<b2时,△ABC是钝角三角形,
即c2<b2-a2=32-22=5,
∴c<
,
∵a<c<b,
∴2<c<
,
∴当2<a<
,时,△ABC是钝角三角形,
③c<a<b
当c2+a2<b2时,△ABC是钝角三角形,
即c2<b2-a2=32-22=5,
∴c<
,
∵c<a<b,
∴0<c<2,
∴当0<c<2时,△ABC是钝角三角形,
∴当c>
或当2<a<
或0<c<2时,△ABC是钝角三角形.
①a<b<c,
当a2+b2>c2时,△ABC是锐角三角形,
即c2<22+32=13,
∴c<
| 13 |
∵a<b<c
∴3<c<
| 13 |
∴当3<c<
| 13 |
②a<c<b
当a2+c2>b2时,△ABC是锐角三角形,
即c2>b2-a2=32-22=5,
∴c>
| 5 |
∵a<c<b,
∴
| 5 |
∴当
| 5 |
③c<a<b
当c2+a2>b2时,△ABC是锐角三角形,
即c2>b2-a2=32-22=5,
∴c>
| 5 |
∵c<a<b,
∴
| 5 |
∴当
| 5 |
| 13 |
(2)分三种情况讨论:①a<b<c,②a<c<b,③c<a<b,
①a<b<c
当a2+b2=c2时,△ABC是直角三角形,
即c2=22+32=13,
∴c=
| 13 |
∴当c=
| 13 |
②a<c<b
当a2+c2=b2时,△ABC是直角三角形,
即c2=b2-a2=32-22=5,
∴c=
| 5 |
∴当c=
| 5 |
③c<a<b
当c2+a2=b2时,△ABC是直角三角形,
即c2=b2-a2=32-22=5,
∴c=
| 5 |
∴当c=
| 5 |
∴当c=
| 13 |
| 5 |
(3)分三种情况讨论:①a<b<c,②a<c<b,③c<a<b,
①a<b<c,
当a2+b2<c2时,△ABC是钝角三角形,
即c2>22+32=13,
∴c>
| 13 |
∵a<b<c
∴c>
| 13 |
∴当c>
| 13 |
②a<c<b
当a2+c2<b2时,△ABC是钝角三角形,
即c2<b2-a2=32-22=5,
∴c<
| 5 |
∵a<c<b,
∴2<c<
| 5 |
∴当2<a<
| 5 |
③c<a<b
当c2+a2<b2时,△ABC是钝角三角形,
即c2<b2-a2=32-22=5,
∴c<
| 5 |
∵c<a<b,
∴0<c<2,
∴当0<c<2时,△ABC是钝角三角形,
∴当c>
| 13 |
| 5 |
点评:此题考查了勾股定理的逆定理的应用,解题的关键是:分三种情况讨论:①a<b<c,②a<c<b,③c<a<b.

练习册系列答案
相关题目
在过去的184天里,我们走过了一段成功、精彩、难忘的世博之旅,73080000位参观者流连忘返,则这个数用科学记数法表示为( )(保留3位有效数字)
| A、73.1×106 |
| B、0.731×108 |
| C、7.31×107 |
| D、7.31×108 |
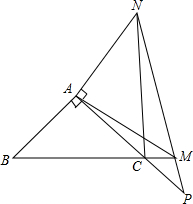 如图,△ABC中,AB=AC,∠B=45°,M是BC延长线上一点,△AMN∽△ABC,MN交AC延长线于点P,连接CN.
如图,△ABC中,AB=AC,∠B=45°,M是BC延长线上一点,△AMN∽△ABC,MN交AC延长线于点P,连接CN.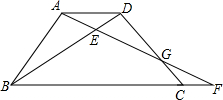 如图,梯形ABCD中,AD∥BC,BC=2AD,点F在BC的延长线上,AF与BD交于点E,AD=2CF,那么△DEG与△CFG的面积比是
如图,梯形ABCD中,AD∥BC,BC=2AD,点F在BC的延长线上,AF与BD交于点E,AD=2CF,那么△DEG与△CFG的面积比是