题目内容
 如图,AB=AC=12,BC=7,∠A=40°,AB的垂直平分线交AB于点交于点D,交AC于点E,△BCE的周长是
如图,AB=AC=12,BC=7,∠A=40°,AB的垂直平分线交AB于点交于点D,交AC于点E,△BCE的周长是考点:线段垂直平分线的性质,等腰三角形的性质
专题:
分析:由AB的垂直平分线交AB于点交于点D,交AC于点E,根据线段垂直平分线的性质,可得AE=BE,继而可得△BCE的周长=AC+BC;又由AB=AC,易求得∠ABC与∠ABE的度数,继而求得∠EBC的度数.
解答:解:∵DE垂直平分AB,
∴AE=BE,
∵AB=AC=12,BC=7,
∴△BCE的周长是:BC+CE+BE=BC+CE+AE=BC+AC=19;
∵AB=AC,AE=BE,∠A=40°,
∴∠ABC=∠C=70°,∠ABE=∠A=40°,
∴∠EBC=∠ABC-∠ABE=30°.
故答案为:19,30°.
∴AE=BE,
∵AB=AC=12,BC=7,
∴△BCE的周长是:BC+CE+BE=BC+CE+AE=BC+AC=19;
∵AB=AC,AE=BE,∠A=40°,
∴∠ABC=∠C=70°,∠ABE=∠A=40°,
∴∠EBC=∠ABC-∠ABE=30°.
故答案为:19,30°.
点评:此题考查了线段垂直平分线的性质以及等腰三角形的性质.此题比较简单,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
在平面直角坐标系中,点A(-1,2)关于y轴的对称点在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知x,y为任意有理数,记M=x2+y2,N=2xy,则M与N的大小关系为( )
| A、M>N | B、M≥N |
| C、M≤N | D、不能确定 |
一个由四舍五入法得到的近似数是4.90,则它精确到( )
| A、个分位 | B、十分位 |
| C、百分位 | D、千分位 |
在过去的184天里,我们走过了一段成功、精彩、难忘的世博之旅,73080000位参观者流连忘返,则这个数用科学记数法表示为( )(保留3位有效数字)
| A、73.1×106 |
| B、0.731×108 |
| C、7.31×107 |
| D、7.31×108 |
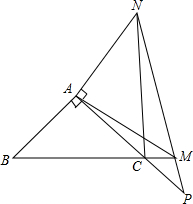 如图,△ABC中,AB=AC,∠B=45°,M是BC延长线上一点,△AMN∽△ABC,MN交AC延长线于点P,连接CN.
如图,△ABC中,AB=AC,∠B=45°,M是BC延长线上一点,△AMN∽△ABC,MN交AC延长线于点P,连接CN.