题目内容
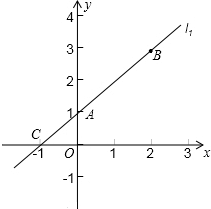 如图,已知直线l1经过点A(0,1)与点B(2,3),另一条直线l2经过点B,且与x轴相交于点P(m,0).
如图,已知直线l1经过点A(0,1)与点B(2,3),另一条直线l2经过点B,且与x轴相交于点P(m,0).(1)求直线l1对应的函数表达式及其与x轴的交点C的坐标;
(2)若△CPB的面积为3,求m的值.
考点:两条直线相交或平行问题
专题:
分析:(1)设直线l1对应的函数表达式为y=kx+b(k≠0),然后利用待定系数法求一次函数解析式解答,再令y=0解方程即可得到点C的坐标;
(2)利用三角形的面积求出PC的长,再分两种情况求出OP,即可得到m的值.
(2)利用三角形的面积求出PC的长,再分两种情况求出OP,即可得到m的值.
解答:解:(1)设直线l1对应的函数表达式为y=kx+b(k≠0),
∵直线l1经过点A(0,1)与点B(2,3),
∴
,
解得
.
∴直线l1对应的函数表达式y=x+1,
令y=0,则x+1=0,
解得x=-1.
所以,点C的坐标为(-1,0);
(2)△CPB的面积=
PC•3=3,
解得PC=2,
当点P在点C的左边时,OP=OC+PC=1+2=3,
此时m=-3,
当点P在点C的右边时,OP=PC-OC=2-1=1,
此时m=1,
综上所述,m的值为1或-3.
∵直线l1经过点A(0,1)与点B(2,3),
∴
|
解得
|
∴直线l1对应的函数表达式y=x+1,
令y=0,则x+1=0,
解得x=-1.
所以,点C的坐标为(-1,0);
(2)△CPB的面积=
| 1 |
| 2 |
解得PC=2,
当点P在点C的左边时,OP=OC+PC=1+2=3,
此时m=-3,
当点P在点C的右边时,OP=PC-OC=2-1=1,
此时m=1,
综上所述,m的值为1或-3.
点评:本题考查了两直线相交的问题,三角形的面积,主要利用了待定系数法求一次函数解析式,注意(2)要分情况讨论.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
已知x,y为任意有理数,记M=x2+y2,N=2xy,则M与N的大小关系为( )
| A、M>N | B、M≥N |
| C、M≤N | D、不能确定 |
 已知△ABC中,D是AC上一点,
已知△ABC中,D是AC上一点, 如图,△ABC中,AB=AC,∠B=45°,M是BC延长线上一点,△AMN∽△ABC,MN交AC延长线于点P,连接CN.
如图,△ABC中,AB=AC,∠B=45°,M是BC延长线上一点,△AMN∽△ABC,MN交AC延长线于点P,连接CN.