题目内容
在平面直角坐标系中,O为坐标原点,△AOB为正三角形,点B的坐标为(2,0),点P是线段OB的三等分点.
(1)求经过A、O两点的直线AO的解析式;
(2)过点P作PC⊥AB,PD⊥AO,垂足分别为C、D,求PC+PD的值;
(3)在(2)的条件下,点E在x轴的负半轴上,作直线CE交AO于点F,且△ACF和△EOF的面积相等,求直线CE的解析式.
(1)求经过A、O两点的直线AO的解析式;
(2)过点P作PC⊥AB,PD⊥AO,垂足分别为C、D,求PC+PD的值;
(3)在(2)的条件下,点E在x轴的负半轴上,作直线CE交AO于点F,且△ACF和△EOF的面积相等,求直线CE的解析式.
考点:一次函数综合题
专题:
分析:(1)根据等边三角形的性质求得点A的坐标,点A的坐标求出以后,即可求得OA所在直线的解析式;
(2)已知PC⊥AB,PD⊥AO,可以根据勾股定理分别求得PC和PD的长度;
(3)根据S△ACF=S△EOF可得S△ACF+S四边形OBCF=S△EOF+S四边形OBCF,即S△ABC=S△BEC.过C点作CM⊥PB,垂足为M,设点P的坐标为(x,0),根据点P是线段OB的三等分点,分为两种情况进行讨论OP=
OB或OP=
OB,再根据三角形的面积公式求得点P和点C的坐标.
(2)已知PC⊥AB,PD⊥AO,可以根据勾股定理分别求得PC和PD的长度;
(3)根据S△ACF=S△EOF可得S△ACF+S四边形OBCF=S△EOF+S四边形OBCF,即S△ABC=S△BEC.过C点作CM⊥PB,垂足为M,设点P的坐标为(x,0),根据点P是线段OB的三等分点,分为两种情况进行讨论OP=
| 1 |
| 3 |
| 2 |
| 3 |
解答:解:(1)∵△AOB为正三角形,点B在x轴上且点B的坐标为(2,0),
∴A点在线段OB的垂直平分线上,
∴A点的横坐标为1,
∴设点A的坐标为(1,y),
∵OA=OB=2
∴
=2,
解得y1=
,y2=-
∴点A的坐标为(1,
)或(1,-
);
∴经过A、O两点的直线AO的解析式为:y=±
x;
(2)根据三角形的面积公式可得S△ABC=S△AOP+S△ABP,
即
OB•AD=
OA•PC+
AB•PD,因为AO=OB=AB,
所以AD=PC+PD,
所以PC+PD=
;
(3)∵S△ACF=S△EOF,
∴S△ACF+S四边形OBCF=S△EOF+S四边形OBCF,即S△ABC=S△BEC,
如图,过C点作CM⊥PB,垂足为M,设点P的坐标为(x,0),
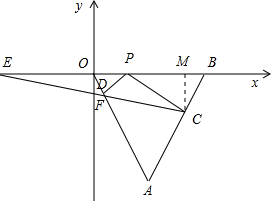
∵点P是线段OB的三等分点,
可分为两种情况进行讨论OP=
OB或OP=
OB,
①当AP=
OB时,即AP=
,BP=2-
=
,
∵∠B=60°,PC⊥AB,可得BC=
,MB=
,
∴CM=
(勾股定理),
由S△ABC=S△BEC,即
OB×AD=
PB×CM,
得
×2×
=
×(2-x)×
,解得x=-4,
∴点P的坐标为(-4,0),
由MB=
,可得OM=OB-MB=
,故点C的坐标为(
,
)或(
,-
),
∴当点C的坐标为(
,
),直线CE的解析式为y=
(x+4),
当点C的坐标为(
,-
),直线CE的解析式为y=-
(x+4);
②当AP=
OB时,同理可求得OM=
,CM=
,x=-10,故点P的坐标为(-10,0),
故点C的坐标为(
,
)或(
,-
),
∴当点C的坐标为(
,
)时,直线CE的解析式为y=
(x+10);
当点C的坐标为(
,-
)时,直线CE的解析式为y=-
(x+10);
综上可知直线CE的解析式为y=
(x+4)或y=-
(x+4)或y=
(x+10)或y=-
(x+10).
∴A点在线段OB的垂直平分线上,
∴A点的横坐标为1,
∴设点A的坐标为(1,y),
∵OA=OB=2
∴
| 12+y2 |
解得y1=
| 3 |
| 3 |
∴点A的坐标为(1,
| 3 |
| 3 |
∴经过A、O两点的直线AO的解析式为:y=±
| 3 |
(2)根据三角形的面积公式可得S△ABC=S△AOP+S△ABP,
即
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以AD=PC+PD,
所以PC+PD=
| 3 |
(3)∵S△ACF=S△EOF,
∴S△ACF+S四边形OBCF=S△EOF+S四边形OBCF,即S△ABC=S△BEC,
如图,过C点作CM⊥PB,垂足为M,设点P的坐标为(x,0),

∵点P是线段OB的三等分点,
可分为两种情况进行讨论OP=
| 1 |
| 3 |
| 2 |
| 3 |
①当AP=
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
∵∠B=60°,PC⊥AB,可得BC=
| 2 |
| 3 |
| 1 |
| 3 |
∴CM=
| ||
| 3 |
由S△ABC=S△BEC,即
| 1 |
| 2 |
| 1 |
| 2 |
得
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
∴点P的坐标为(-4,0),
由MB=
| 1 |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
| ||
| 3 |
| 5 |
| 3 |
| ||
| 3 |
∴当点C的坐标为(
| 5 |
| 3 |
| ||
| 3 |
| ||
| 17 |
当点C的坐标为(
| 5 |
| 3 |
| ||
| 3 |
| ||
| 17 |
②当AP=
| 2 |
| 3 |
| 11 |
| 6 |
| ||
| 6 |
故点C的坐标为(
| 11 |
| 6 |
| ||
| 6 |
| 11 |
| 6 |
| ||
| 6 |
∴当点C的坐标为(
| 11 |
| 6 |
| ||
| 6 |
| ||
| 71 |
当点C的坐标为(
| 11 |
| 6 |
| ||
| 6 |
| ||
| 71 |
综上可知直线CE的解析式为y=
| ||
| 17 |
| ||
| 17 |
| ||
| 71 |
| ||
| 71 |
点评:本题主要考查待定系数法求函数解析及等边三角形、直角三角形等知识的综合应用,求函数解析式先求出点的坐标这是解题的常用方法,在求第(3)问时注意需要分点P是哪个三等分点来讨论.

练习册系列答案
相关题目
一个由四舍五入法得到的近似数是4.90,则它精确到( )
| A、个分位 | B、十分位 |
| C、百分位 | D、千分位 |
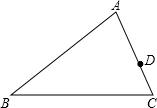 已知△ABC中,D是AC上一点,
已知△ABC中,D是AC上一点,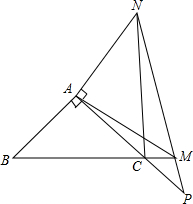 如图,△ABC中,AB=AC,∠B=45°,M是BC延长线上一点,△AMN∽△ABC,MN交AC延长线于点P,连接CN.
如图,△ABC中,AB=AC,∠B=45°,M是BC延长线上一点,△AMN∽△ABC,MN交AC延长线于点P,连接CN.



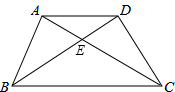 如图,在四边形ABCD中,AB=AD,AC与BD交于点E,∠ADB=∠ACB.
如图,在四边形ABCD中,AB=AD,AC与BD交于点E,∠ADB=∠ACB.