题目内容
20.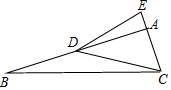 已知:如图,在△ABC中,∠BAC=90°,点D在AB上,点E在CA的延长线上,连接DC、DE,∠EDC=45°,BD=EC,DE=5$\sqrt{2}$,tan∠DCE=$\frac{3}{13}$,则CE=$\frac{5\sqrt{18}}{3}$.
已知:如图,在△ABC中,∠BAC=90°,点D在AB上,点E在CA的延长线上,连接DC、DE,∠EDC=45°,BD=EC,DE=5$\sqrt{2}$,tan∠DCE=$\frac{3}{13}$,则CE=$\frac{5\sqrt{18}}{3}$.
分析 过E作EF⊥CD于F,解直角三角形即可得到结论.
解答  解:过E作EF⊥CD于F,
解:过E作EF⊥CD于F,
∵∠EDC=45°,
∴EF=DF=$\frac{\sqrt{2}}{2}$DE,
∵DE=5$\sqrt{2}$,
∴EF=5,
∵tan∠DCE=$\frac{EF}{CF}$=$\frac{3}{13}$,
∴CF=$\frac{65}{3}$,
∴CE=$\sqrt{E{F}^{2}+C{F}^{2}}$=$\sqrt{{5}^{2}+(\frac{65}{3})^{2}}$=$\frac{5\sqrt{18}}{3}$,
故答案为:$\frac{5\sqrt{18}}{3}$.
点评 本题考查了解直角三角形,正确的作出辅助线构造直角三角形是解题的关键.

练习册系列答案
相关题目
3.4的平方根是( )
| A. | 16 | B. | 2 | C. | ±2 | D. | $±\sqrt{2}$ |
12.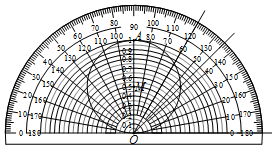 利用量角器可以制作“锐角正弦值速查卡”.制作方法如下:如图,设OA=1,以O为圆心,分别以0.05,0.1,0.15,0.2,…,0.9,0.95长为半径作半圆,再以OA为直径作⊙M.利用“锐角正弦值速查卡”可以读出相应锐角正弦的近似值.例如:sin60°≈0.87,sin45°=0.71.下列角度中正弦值最接近0.94的是( )
利用量角器可以制作“锐角正弦值速查卡”.制作方法如下:如图,设OA=1,以O为圆心,分别以0.05,0.1,0.15,0.2,…,0.9,0.95长为半径作半圆,再以OA为直径作⊙M.利用“锐角正弦值速查卡”可以读出相应锐角正弦的近似值.例如:sin60°≈0.87,sin45°=0.71.下列角度中正弦值最接近0.94的是( )
 利用量角器可以制作“锐角正弦值速查卡”.制作方法如下:如图,设OA=1,以O为圆心,分别以0.05,0.1,0.15,0.2,…,0.9,0.95长为半径作半圆,再以OA为直径作⊙M.利用“锐角正弦值速查卡”可以读出相应锐角正弦的近似值.例如:sin60°≈0.87,sin45°=0.71.下列角度中正弦值最接近0.94的是( )
利用量角器可以制作“锐角正弦值速查卡”.制作方法如下:如图,设OA=1,以O为圆心,分别以0.05,0.1,0.15,0.2,…,0.9,0.95长为半径作半圆,再以OA为直径作⊙M.利用“锐角正弦值速查卡”可以读出相应锐角正弦的近似值.例如:sin60°≈0.87,sin45°=0.71.下列角度中正弦值最接近0.94的是( )| A. | 70° | B. | 50° | C. | 40° | D. | 30° |
9.在综合实践话动课上,老师组织大家利用两块大小相同的含30°角的三角板进行拼接组合(不重叠)的探索活动,在讨论所组合而成的图形过程中,所得下列四个结论中错误的是( )
| A. | 当两块三角板的斜边完全拼接在一起时,所拼成的图形一定是轴对称图形 | |
| B. | 当两块三角板的对应直角边完全拼接在一起时,所拼成的图形可能是等边三角形 | |
| C. | 当两块三角板可以通过平移后重合时,所拼成的图形不可能是轴对称图形 | |
| D. | 当两块三角板只有直角顶点拼接在一起时,所拼成的图形不可能是中心对称图形 |
10.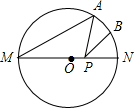 如图,MN是⊙O的直径,MN=4,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
如图,MN是⊙O的直径,MN=4,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
 如图,MN是⊙O的直径,MN=4,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
如图,MN是⊙O的直径,MN=4,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 3 |
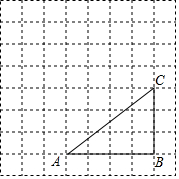 如图,将△ABC放在由小正方形构成的网格图中,点A、B、C均落在格点上.
如图,将△ABC放在由小正方形构成的网格图中,点A、B、C均落在格点上. 已知:二次函数y=2x2+4x+m-1,与x轴的公共点为A,B.
已知:二次函数y=2x2+4x+m-1,与x轴的公共点为A,B.