题目内容
5.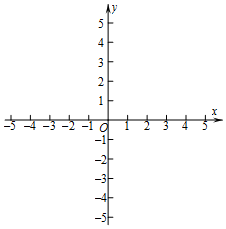 已知:二次函数y=2x2+4x+m-1,与x轴的公共点为A,B.
已知:二次函数y=2x2+4x+m-1,与x轴的公共点为A,B.(1)如果A与B重合,求m的值;
(2)横、纵坐标都是整数的点叫做整点;
①当m=1时,求线段AB上整点的个数;
②若设抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)整点的个数为n,当1<n<8时,结合函数的图象,求m的取值范围.
分析 (1)当A、B重合时,抛物线与x轴只有一个交点,此时△=0,从可求出m的值.
(2)①m=1代入抛物线解析式,然后求出该抛物线与x轴的两个交点的坐标,从而可求出线段AB上的整点;
②根据二次函数表达式可以用带m表达出两根之差,根据1<两根之差<8,即可解题.
解答 解:(1)∵A与B重合,
∴二次函数y=2x2+4x+m-1的图象与x轴只有一个公共点,
∴方程2x2+4x+m-1=0有两个相等的实数根,
∴△=42-4×2(m-1)=24-8m=0,
解得:m=3.
∴如果A与B重合,m的值为3.
(2)①当m=1时,原二次函数为y=2x2+4x+m-1=2x2+4x,
令y=2x2+4x=0,则x1=0,x2=-2,
∴线段AB上的整点有(-2,0)、(-1,0)和(0,0).
故当m=1时,线段AB上整点的个数有3个.
②由点A,B之间的部分与线段AB所围成的区域内(包括边界)可用以下不等式表示
(3)如图,
对于二次函数y=2x2+4x+m-1,可知对称轴x=-1,
∵抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)整点的个数为n,且1<n<8,
∴x=0时,y≤0;x=3时,y>0;
则有$\left\{\begin{array}{l}{m-1≤0}\\{18+12+m-1>0}\end{array}\right.$,
解得:-29<m≤1.
点评 本题考查了二次函数求根公式的应用,考查了二次函数只有一个根时△=0的应用,熟练解二次函数是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
8.不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征.甲同学:它有4个面是三角形;乙同学:它有8条棱.该模型的形状对应的立体图形可能是( )
| A. | 三棱柱 | B. | 四棱柱 | C. | 三棱锥 | D. | 四棱锥 |
15.把0.17×105改写成科学记数法的形式,正确的是( )
| A. | 17×103 | B. | 17×104 | C. | 1.7×104 | D. | 1.7×106 |
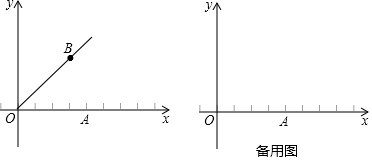
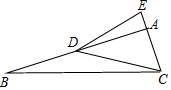 已知:如图,在△ABC中,∠BAC=90°,点D在AB上,点E在CA的延长线上,连接DC、DE,∠EDC=45°,BD=EC,DE=5$\sqrt{2}$,tan∠DCE=$\frac{3}{13}$,则CE=$\frac{5\sqrt{18}}{3}$.
已知:如图,在△ABC中,∠BAC=90°,点D在AB上,点E在CA的延长线上,连接DC、DE,∠EDC=45°,BD=EC,DE=5$\sqrt{2}$,tan∠DCE=$\frac{3}{13}$,则CE=$\frac{5\sqrt{18}}{3}$.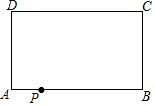 如图矩形ABCD中AB=6,AD=4,点P为AB上一点,把矩形ABCD沿过P点的直线l折叠,使D点落在BC边上的D′处,直线l与CD边交于Q点.
如图矩形ABCD中AB=6,AD=4,点P为AB上一点,把矩形ABCD沿过P点的直线l折叠,使D点落在BC边上的D′处,直线l与CD边交于Q点.