题目内容
4.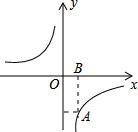 如图,函数y=$\frac{k}{x}$的图象经过点A(1,-3),AB垂直x轴于点B,则下列说法正确的是( )
如图,函数y=$\frac{k}{x}$的图象经过点A(1,-3),AB垂直x轴于点B,则下列说法正确的是( )| A. | k=3 | B. | x<0时,y随x增大而增大 | ||
| C. | S△AOB=3 | D. | 函数图象关于y轴对称 |
分析 首先把(1,-3)代入反比例函数关系式,可得k的值,进而可得A错误,根据反比例函数的性质:当k<0时,在每一个象限内,函数值y随自变量x增大而增大可得B正确,根据三角形的面积公式可C错误;根据反比例函数的性质可得D错误.
解答 解:∵函数y=$\frac{k}{x}$的图象经过点A(1,-3),
∴-3=$\frac{k}{1}$,
解得:k=-3,
故A错误;
∵k<0,
∴x<0时,y随x增大而增大,
故B正确;
∵点A(1,-3),AB垂直x轴于点B,
∴S△AOB=3×1×$\frac{1}{2}$=$\frac{3}{2}$,
故C错误;
反比例函数图象关于原点对称,故D错误;
故选:B.
点评 此题主要考查了反比例函数的性质,关键是掌握反比例函数的性质:
(1)反比例函数y=$\frac{k}{x}$(k≠0)的图象是双曲线;
(2)当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;
(3)当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.
注意:反比例函数的图象与坐标轴没有交点.

练习册系列答案
相关题目
13.下列运算不正确的是( )
| A. | x6÷x3=x3 | B. | (-x3)4=x12 | C. | x2•x3=x5 | D. | x3+x3=x6 |
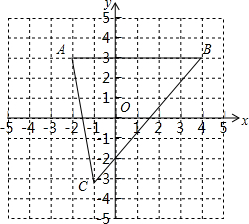 如图,已知A(-2,3)、B(4,3)、C(-1,-3).
如图,已知A(-2,3)、B(4,3)、C(-1,-3). 如图,矩形空地的长为13米,宽为8米,计划在其中修建两块相同的矩形绿地,它们的面积之和为28平方米,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米?
如图,矩形空地的长为13米,宽为8米,计划在其中修建两块相同的矩形绿地,它们的面积之和为28平方米,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米? 如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=35°,求∠BAC的度数.
如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=35°,求∠BAC的度数.