题目内容
7.(1)分解因式:16x3-x;(2)已知a=2+$\sqrt{3}$,b=2-$\sqrt{3}$,求代数式$\frac{a}{b}$-$\frac{b}{a}$的值.
分析 (1)先提取公因式,再根据平方差公式进行分解即可;
(2)先求出a+b,a-b及ab的值,再代入代数式进行计算即可.
解答 解:(1)原式=x(16x2-1)
=x(4x+1)(4x-1);
(2)∵a=2+$\sqrt{3}$,b=2-$\sqrt{3}$,
∴a+b=4,ab=-1,a-b=2$\sqrt{3}$,
∴原式=$\frac{{a}^{2}-{b}^{2}}{ab}$=$\frac{(a+b)(a-b)}{ab}$=$\frac{4×2\sqrt{3}}{1}$=8$\sqrt{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
2.已知a=$\frac{1}{2+\sqrt{3}}$,b=2-$\sqrt{3}$,则a与b的大小关系是( )
| A. | a>b | B. | a=b | C. | a<b | D. | 不确定 |
17. 如图所示的四条射线中,表示南偏东65°的是( )
如图所示的四条射线中,表示南偏东65°的是( )
 如图所示的四条射线中,表示南偏东65°的是( )
如图所示的四条射线中,表示南偏东65°的是( )| A. | 射线OA | B. | 射线OB | C. | 射线OC | D. | 射线OD |
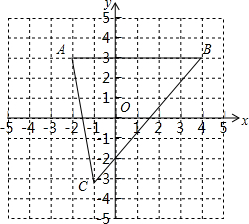 如图,已知A(-2,3)、B(4,3)、C(-1,-3).
如图,已知A(-2,3)、B(4,3)、C(-1,-3).