题目内容
9.如图,边长为4的等边三角形ABC是三棱锥的一个横截面,一束光线沿着与AB边垂直的方向射入到BC边上的D点处(D与B,C 两点不重合),反射光线又从边AC射出去,DK为法线,设BE的长为x,AF的长为y.(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)在给出的平面直角坐标系中画出该函数的图象.

分析 (1)由直角三角形30°角所对的边等于斜边的一半得到BD=2x,CD=4-2x,根据等角的余角相等得到∠1=∠2=30°,进而CF=2-x,可得y=4-CF=x+2;
(2)由(0,2)、(2,4)两点在y=x+2上,结合0<x<2可画出函数图象;
解答 解:(1)∵△ABC是边长等于4的等边三角形,
∴∠B=∠C=60°,AB=BC=CA=4,
∵MD⊥AB于E,∴∠1=30°.
∵BE的长为x,∴BD=2x,
∴DC=4-2x,
∵DK为法线,∴KD⊥BC,∠3和∠4分别为入射角和反射角,
∴∠3=∠4,
∴∠1=∠2=30°.
∴∠DFC=90°.
∴FC=2-x,
∴AF=4-(2-x)=x+2=y.
∴y 和 x 之间的函数关系式是 y=x+2,
自变量 x 的取值范围是 0<x<2.
(2)函数图象如下:
点评 本题考查了等边三角形的性质、直角三角形30°角所对的直角边等于斜边的一半的性质等,有一定综合性,属中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
17. 如图所示的四条射线中,表示南偏东65°的是( )
如图所示的四条射线中,表示南偏东65°的是( )
 如图所示的四条射线中,表示南偏东65°的是( )
如图所示的四条射线中,表示南偏东65°的是( )| A. | 射线OA | B. | 射线OB | C. | 射线OC | D. | 射线OD |
4. 如图,E是△ABC的内心,若∠BEC=130°,则∠A的度数是( )
如图,E是△ABC的内心,若∠BEC=130°,则∠A的度数是( )
 如图,E是△ABC的内心,若∠BEC=130°,则∠A的度数是( )
如图,E是△ABC的内心,若∠BEC=130°,则∠A的度数是( )| A. | 60° | B. | 80° | C. | 50° | D. | 75° |
18.为完成下列任务,最适合用普查的是( )
| A. | 了解全国七年级学生的视力情况 | B. | 对乘坐高铁的乘客进行安检 | ||
| C. | 了解一批电视机的使用寿命 | D. | 检测汾河某段水域的水质情况 |
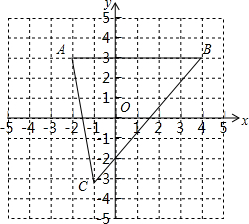 如图,已知A(-2,3)、B(4,3)、C(-1,-3).
如图,已知A(-2,3)、B(4,3)、C(-1,-3). 如图,AB为⊙O的直径,AE为⊙O的切线,若tan∠ABE=$\frac{1}{2}$,AE=3,求BD的长.
如图,AB为⊙O的直径,AE为⊙O的切线,若tan∠ABE=$\frac{1}{2}$,AE=3,求BD的长. 如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=35°,求∠BAC的度数.
如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=35°,求∠BAC的度数. 如图所示,现有下列4个亊项:
如图所示,现有下列4个亊项: