题目内容
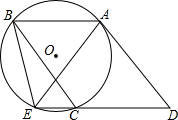 如图,△ABC内接于⊙O,CD∥AB,AD∥BC,DC的延长线交⊙O于E,连接BE、AE.
如图,△ABC内接于⊙O,CD∥AB,AD∥BC,DC的延长线交⊙O于E,连接BE、AE.(1)判断△ADE的形状,并说明理由;
(2)若CD=BE,求证:AD是⊙O的切线.
考点:切线的判定
专题:
分析:(1)利用平行四边形的判定以及平行弦的性质得出AE=AD,即可得出答案;
(2)利用已知,得出∠DAC=∠AFC,进而得出∠FAD=90°,即可得出答案.
(2)利用已知,得出∠DAC=∠AFC,进而得出∠FAD=90°,即可得出答案.
解答: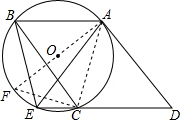 (1)解:△ADE是等腰三角形,
(1)解:△ADE是等腰三角形,
理由:∵CD∥AB,AD∥BC,
∴四边形BCDA是平行四边形,
∴BC=AD,
∵CD∥AB,
∴
=
,
∴
=
,
∴BC=AE,
∴AE=AD,
∴△ADE是等腰三角形;
(2)证明:连接AO并延长交⊙O于F,连接CF,AC,
∵CD∥AB,
∴
=
,
∴AC=BE,
∵CD=BE,
∴AC=CD,
∴∠D=∠CAD,
∵∠D=∠AED,∠AED=∠AFC,
∴∠DAC=∠AFC,
∵AF是直径,
∴∠ACF=90°,
∴∠AFC+∠FAC=90°,
∴∠FAC+∠DAC=90°,
∴∠FAD=90°,
∴AD是⊙O的切线.
 (1)解:△ADE是等腰三角形,
(1)解:△ADE是等腰三角形,理由:∵CD∥AB,AD∥BC,
∴四边形BCDA是平行四边形,
∴BC=AD,
∵CD∥AB,
∴
 |
| BE |
 |
| AC |
∴
 |
| BC |
 |
| AE |
∴BC=AE,
∴AE=AD,
∴△ADE是等腰三角形;
(2)证明:连接AO并延长交⊙O于F,连接CF,AC,
∵CD∥AB,
∴
 |
| BE |
 |
| AC |
∴AC=BE,
∵CD=BE,
∴AC=CD,
∴∠D=∠CAD,
∵∠D=∠AED,∠AED=∠AFC,
∴∠DAC=∠AFC,
∵AF是直径,
∴∠ACF=90°,
∴∠AFC+∠FAC=90°,
∴∠FAC+∠DAC=90°,
∴∠FAD=90°,
∴AD是⊙O的切线.
点评:此题主要考查了切线的判定以及平行四边形的判定与性质以及平行弦的性质,得出
=
是解题关键.
 |
| AC |
 |
| BE |

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
下列各式中,从左到右的变形是因式分解的是( )
| A、3x+3y-5=3(x+y)-5 |
| B、(x+1)(x-1)=x2-1 |
| C、x2+2x+1=(x+1)2 |
| D、x(x-y)=x2-xy |
下列各数中,是负数的是( )
| A、-(-3) | B、-|-3| |
| C、(-3) | D、|-3| |
 已知A、B两点在数轴上表示的数为a和b,M、N均为数轴上的点,且OA<OB.
已知A、B两点在数轴上表示的数为a和b,M、N均为数轴上的点,且OA<OB.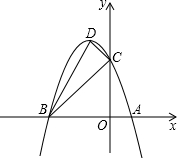 如图,抛物线与x轴交于A(1,0)、B(-3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.坐标轴上有一动点P,使得以P、A、C为顶点的三角形与△BCD相似.则点P的坐标
如图,抛物线与x轴交于A(1,0)、B(-3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.坐标轴上有一动点P,使得以P、A、C为顶点的三角形与△BCD相似.则点P的坐标