题目内容
4.已知x1,x2是方程x2-2x+a=0的两个实数根,且x1+2x2=3-$\sqrt{2}$.则x13-3x12+2x1+x2的值为1.分析 根据x1,x2是方程x2-2x+a=0的两个实数根,得出x1+x2=2,再根据x1+2x2=3-$\sqrt{2}$,求出x2和x1,根据x1x2=a,求出a,最后根据x13-3x12+2x1+x2=x1(x12-2x1)-(x12-2x1)+x2,代入计算即可.
解答 解:∵x1,x2是方程x2-2x+a=0的两个实数根,
∴x1+x2=2,
∵x1+2x2=3-$\sqrt{2}$,
∴x2=1-$\sqrt{2}$,x1=1+$\sqrt{2}$,
∴x1x2=a=-1,
∵x12-2x1+a=0,
∴x12-2x1=-a
∴x13-3x12+2x1+x2
=x13-2x12-x12+2x1+x2
=x1(x12-2x1)-(x12-2x1)+x2
=x1•(-a)+a+x2
=(x1+x2)-1
=2-1
=1.
故答案为:1
点评 此题考查一元二次方程根与系数的关系:x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
相关题目
12.下列说法正确的是( )
| A. | 一组数据8,8,7,10,6,8,9的众数和中位数都是8 | |
| B. | 为了解全国中学生的心理健康情况,应该采用普查的方式 | |
| C. | 一个游戏的中奖概率是0.1,则做10次这样的游戏一定会中奖 | |
| D. | 若甲组数据的方差s2=0.01,乙组数据的方差s2=0.1,则乙组数据比甲组数据稳定 |
19.若x轴上的点P到y轴的距离为2015,则点P的坐标是( )
| A. | (2015,0) | B. | (0,2015) | C. | (2015,0)或(-2015,0) | D. | (0,2015)或(0,-2015) |

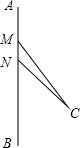 “村村通公路”工程是国家为支持新农村建设的一项重大举措,为了落实这一举措,重庆潼南县政府计划在南北方向的A、B两村之间建一条公路AB.已知公路AB的一侧有C村,在公路AB上的M处测得C村在M的南偏东37°方向上,从M向南走270米到达N处,测得C村在N的东南方向上,且C村周围800米范围内为油菜花田,那么计划修建的公路AB是否会穿过油菜花田,请说明理由(参考数据:sin37°≈0.8,cos37°≈0.8,tan37°≈0.75)
“村村通公路”工程是国家为支持新农村建设的一项重大举措,为了落实这一举措,重庆潼南县政府计划在南北方向的A、B两村之间建一条公路AB.已知公路AB的一侧有C村,在公路AB上的M处测得C村在M的南偏东37°方向上,从M向南走270米到达N处,测得C村在N的东南方向上,且C村周围800米范围内为油菜花田,那么计划修建的公路AB是否会穿过油菜花田,请说明理由(参考数据:sin37°≈0.8,cos37°≈0.8,tan37°≈0.75)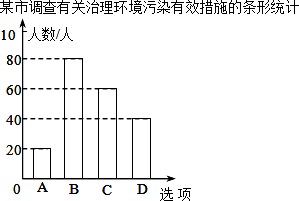 某市对市民进行了有关“治理环境污染”的问卷调查,调查问卷内容是“你认为下列哪种治理环境污染的措施最有效?”有以下四个选项(每份调查问卷必答且只选一个选项):
某市对市民进行了有关“治理环境污染”的问卷调查,调查问卷内容是“你认为下列哪种治理环境污染的措施最有效?”有以下四个选项(每份调查问卷必答且只选一个选项):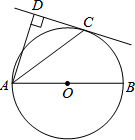 如图,AB是⊙O的直径,C是⊙O上一点,AD垂直与过点C的直线,垂足为D,AC平分∠BAD.
如图,AB是⊙O的直径,C是⊙O上一点,AD垂直与过点C的直线,垂足为D,AC平分∠BAD.