题目内容
5.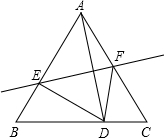 如图所示,等边三角形ABC的边长是4,点D在BC边上移动,连接AD,作AD的垂直平分线,分别与边AB、AC相交于点E、F,连接DE、DF.
如图所示,等边三角形ABC的边长是4,点D在BC边上移动,连接AD,作AD的垂直平分线,分别与边AB、AC相交于点E、F,连接DE、DF.(1)设BD=x,试用含x的代数式表示△BDE和△CDF的周长;
(2)在点D的移动过程中,△BDE和△CDF的周长能否相等?如果能,指出点D在BC边的什么位置;如果不能,试简单说明理由.
分析 (1)先用CD表示出BD,然后再利用线段垂直平分线上的点到线段两端点的距离相等得到AE=DE,所以△BDE的周长等于AB+BD,整理即可;
(2)要使△BDE和△CDF的周长相等,则4+x=8-x,解方程即可求得BD的长,进而求得DC的长,从而判定D的位置.
解答 解:(1)∵BD=x,BC=4,
∴CD=4-x.
∵EF是AD的垂直平分线,
∴DE=AE,AF=DF,
∴C△BDE=AB+BD,C△CDF=AC+CD
即C△BDE=4+x,C△CDF=4+4-x=8-x,
(2)要使△BDE和△CDF的周长相等,则4+x=8-x,
解得x=2,
∴BD=CD,
∴点D在BC边的中点位置时,△BDE和△CDF的周长相等.
点评 本题考查了等边三角形的性质,线段垂直平分线上的点到线段两端点的距离相等的性质,熟练掌握这些性质是解题的关键.

练习册系列答案
相关题目
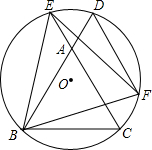 如图,△ABC是等边三角形,⊙O过B、C两点,与BA、CA的延长线分别交于点D、E,弦DF∥AC交⊙O于点F,连结BE、BF、EF.试判断△BEF的形状,并说明理由.
如图,△ABC是等边三角形,⊙O过B、C两点,与BA、CA的延长线分别交于点D、E,弦DF∥AC交⊙O于点F,连结BE、BF、EF.试判断△BEF的形状,并说明理由.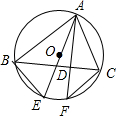 已知:如图,△ABC内接于⊙O,AF是⊙O的弦,AF⊥BC,垂足为D,点E为弧BF上一点,且BE=CF,
已知:如图,△ABC内接于⊙O,AF是⊙O的弦,AF⊥BC,垂足为D,点E为弧BF上一点,且BE=CF,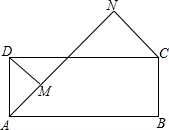 如图,矩形ABCD中,AB>AD,AB=10cm,AN平分∠DAB,DM⊥AN于点M,CN⊥AN于点N,则DM+CN=5$\sqrt{2}$cm.
如图,矩形ABCD中,AB>AD,AB=10cm,AN平分∠DAB,DM⊥AN于点M,CN⊥AN于点N,则DM+CN=5$\sqrt{2}$cm.