题目内容
12.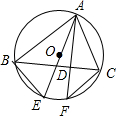 已知:如图,△ABC内接于⊙O,AF是⊙O的弦,AF⊥BC,垂足为D,点E为弧BF上一点,且BE=CF,
已知:如图,△ABC内接于⊙O,AF是⊙O的弦,AF⊥BC,垂足为D,点E为弧BF上一点,且BE=CF,(1)求证:AE是⊙O的直径;
(2)若∠ABC=∠EAC,AE=8,求AC的长.
分析 (1)由BE=CF,则可证得∠BAE=∠FAC,根据圆周角定理和等角的余角相等证明即可;
(2)连接OC,根据圆周角定理证明△AOC是等腰直角三角形,由勾股定理即可求得.
解答 (1)证明:∵BE=CF,
∴$\widehat{BE}$=$\widehat{CF}$,
∴∠BAE=∠CAF,
∵AF⊥BC,
∴ADC=90°,
∴∠FAD+∠ACD=90°,
∵∠E=∠ACB,
∴∠E+∠BAE=90°,
∴∠ABE=90°,
∴AE是⊙O的直径;
(2)如图 ,连接OC,
,连接OC,
∴∠AOC=2∠ABC,
∵∠ABC=∠CAE,
∴∠AOC=2∠CAE,
∵OA=OA,
∴∠CAO=∠ACO=$\frac{1}{2}$∠AOC,
∴△AOC是等腰直角三角形,
∵AE=8,∴AO=CO=4,
∴AC=4$\sqrt{2}$.
点评 本题考查了圆周角定理和其推论:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.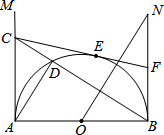 如图,AB是半圆O的直径,射线AM、BN为半圆的切线.在AM上取一点C,连接BC交半圆于点D,连接AD.过O点作BC的垂线ON,与BN相交于点N.过C点作半圆的切线CE,切点为E,与BN相交于点F.当C在AM上移动时(A点除外),设$\frac{BF}{BN}=n$,则n的值为( )
如图,AB是半圆O的直径,射线AM、BN为半圆的切线.在AM上取一点C,连接BC交半圆于点D,连接AD.过O点作BC的垂线ON,与BN相交于点N.过C点作半圆的切线CE,切点为E,与BN相交于点F.当C在AM上移动时(A点除外),设$\frac{BF}{BN}=n$,则n的值为( )
 如图,AB是半圆O的直径,射线AM、BN为半圆的切线.在AM上取一点C,连接BC交半圆于点D,连接AD.过O点作BC的垂线ON,与BN相交于点N.过C点作半圆的切线CE,切点为E,与BN相交于点F.当C在AM上移动时(A点除外),设$\frac{BF}{BN}=n$,则n的值为( )
如图,AB是半圆O的直径,射线AM、BN为半圆的切线.在AM上取一点C,连接BC交半圆于点D,连接AD.过O点作BC的垂线ON,与BN相交于点N.过C点作半圆的切线CE,切点为E,与BN相交于点F.当C在AM上移动时(A点除外),设$\frac{BF}{BN}=n$,则n的值为( )| A. | n=$\frac{1}{2}$ | B. | 0<n≤$\frac{3}{4}$ | C. | $\frac{1}{2}$≤n<1 | D. | 无法确定 |
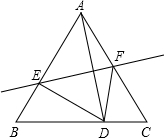 如图所示,等边三角形ABC的边长是4,点D在BC边上移动,连接AD,作AD的垂直平分线,分别与边AB、AC相交于点E、F,连接DE、DF.
如图所示,等边三角形ABC的边长是4,点D在BC边上移动,连接AD,作AD的垂直平分线,分别与边AB、AC相交于点E、F,连接DE、DF.
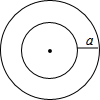 某圆环由圆心相同的两个圆组成,其示意图如图所示,两个圆的面积分别为251.2cm2和62.8cm2,则圆环的宽度a为($4\sqrt{5}-\sqrt{2}$)cm..(π=3.14,结果保留根号)
某圆环由圆心相同的两个圆组成,其示意图如图所示,两个圆的面积分别为251.2cm2和62.8cm2,则圆环的宽度a为($4\sqrt{5}-\sqrt{2}$)cm..(π=3.14,结果保留根号)