题目内容
20.如果四边形ABCD的对角线AC,BD相等,且互相平分于点O,则四边形ABCD是矩形,如果∠AOB=60°,则AB:AC=$\sqrt{3}$:3.分析 由四边形的对角线相等且平分可判定其为矩形,由矩形的性质可知OB=OC,可求得∠ACB=30°,在Rt△ABC中,由三角函数定义可求得AB:AC.
解答 解:∵AC=BD,且互相平分,
∴四边形ABCD为矩形,
∴OC=OB=OA=OD,
∴∠OBC=∠ACB,
∵∠AOB=60°,
∴∠ACB=30°,
在Rt△ABC中,tan∠ACB=$\frac{AB}{AC}$,
∴$\frac{AB}{AC}$=$\frac{\sqrt{3}}{3}$,
故答案为:矩;$\sqrt{3}$:3.
点评 本题主要考查矩形的性质和判定,掌握矩形的对角线相等且平分是解题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
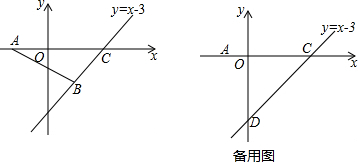
 如图是一张长方形纸条折成的形状,如∠1=105°,求∠2的度数.
如图是一张长方形纸条折成的形状,如∠1=105°,求∠2的度数.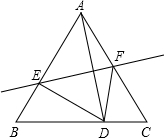 如图所示,等边三角形ABC的边长是4,点D在BC边上移动,连接AD,作AD的垂直平分线,分别与边AB、AC相交于点E、F,连接DE、DF.
如图所示,等边三角形ABC的边长是4,点D在BC边上移动,连接AD,作AD的垂直平分线,分别与边AB、AC相交于点E、F,连接DE、DF.
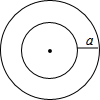 某圆环由圆心相同的两个圆组成,其示意图如图所示,两个圆的面积分别为251.2cm2和62.8cm2,则圆环的宽度a为($4\sqrt{5}-\sqrt{2}$)cm..(π=3.14,结果保留根号)
某圆环由圆心相同的两个圆组成,其示意图如图所示,两个圆的面积分别为251.2cm2和62.8cm2,则圆环的宽度a为($4\sqrt{5}-\sqrt{2}$)cm..(π=3.14,结果保留根号)