题目内容
9.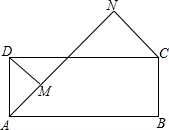 如图,矩形ABCD中,AB>AD,AB=10cm,AN平分∠DAB,DM⊥AN于点M,CN⊥AN于点N,则DM+CN=5$\sqrt{2}$cm.
如图,矩形ABCD中,AB>AD,AB=10cm,AN平分∠DAB,DM⊥AN于点M,CN⊥AN于点N,则DM+CN=5$\sqrt{2}$cm.
分析 根据“AN平分∠DAB,DM⊥AN于点M,CN⊥AN于点N”得出∠MDC=∠NCD=45°,cos45°=$\frac{DM}{DE}=\frac{CN}{CE}$,推出DM+CN=CDcos45°;再根据四边形ABCD是矩形,AB=CD=10cm,DM+CN的值即可求出.
解答 解:∵AN平分∠DAB,DM⊥AN于点M,CN⊥AN于点N,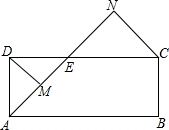
∴∠ADM=∠MDC=∠NCD=45°,
∴$\frac{DM}{cos45°}+\frac{CN}{cos45°}$=CD,
在矩形ABCD中,AB=CD=a,
∴DM+CN=CD×cos45°=$\frac{\sqrt{2}}{2}$×10=5$\sqrt{2}$cm.
故答案为:5$\sqrt{2}$.
点评 本题主要考查了利用角平分线的性质,矩形的性质,锐角三角函数的定义,等腰直角三角形的性质等知识点的理解和掌握,灵活地运用性质进行计算是解此题的关键.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
17.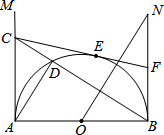 如图,AB是半圆O的直径,射线AM、BN为半圆的切线.在AM上取一点C,连接BC交半圆于点D,连接AD.过O点作BC的垂线ON,与BN相交于点N.过C点作半圆的切线CE,切点为E,与BN相交于点F.当C在AM上移动时(A点除外),设$\frac{BF}{BN}=n$,则n的值为( )
如图,AB是半圆O的直径,射线AM、BN为半圆的切线.在AM上取一点C,连接BC交半圆于点D,连接AD.过O点作BC的垂线ON,与BN相交于点N.过C点作半圆的切线CE,切点为E,与BN相交于点F.当C在AM上移动时(A点除外),设$\frac{BF}{BN}=n$,则n的值为( )
 如图,AB是半圆O的直径,射线AM、BN为半圆的切线.在AM上取一点C,连接BC交半圆于点D,连接AD.过O点作BC的垂线ON,与BN相交于点N.过C点作半圆的切线CE,切点为E,与BN相交于点F.当C在AM上移动时(A点除外),设$\frac{BF}{BN}=n$,则n的值为( )
如图,AB是半圆O的直径,射线AM、BN为半圆的切线.在AM上取一点C,连接BC交半圆于点D,连接AD.过O点作BC的垂线ON,与BN相交于点N.过C点作半圆的切线CE,切点为E,与BN相交于点F.当C在AM上移动时(A点除外),设$\frac{BF}{BN}=n$,则n的值为( )| A. | n=$\frac{1}{2}$ | B. | 0<n≤$\frac{3}{4}$ | C. | $\frac{1}{2}$≤n<1 | D. | 无法确定 |
14.一项“过关游戏”规定:在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷n次,若n次抛掷所出现的点数之和大于$\frac{5}{4}$n2,则算过关;否则不算过关,则能过第2关的概率是( )
| A. | $\frac{13}{18}$ | B. | $\frac{5}{18}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{9}$ |
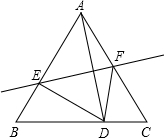
19. 如图,△ABC的高CD和高BE相交于D,则与△DOB相似的三角形个数是( )
如图,△ABC的高CD和高BE相交于D,则与△DOB相似的三角形个数是( )
 如图,△ABC的高CD和高BE相交于D,则与△DOB相似的三角形个数是( )
如图,△ABC的高CD和高BE相交于D,则与△DOB相似的三角形个数是( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
 如图所示,等边三角形ABC的边长是4,点D在BC边上移动,连接AD,作AD的垂直平分线,分别与边AB、AC相交于点E、F,连接DE、DF.
如图所示,等边三角形ABC的边长是4,点D在BC边上移动,连接AD,作AD的垂直平分线,分别与边AB、AC相交于点E、F,连接DE、DF.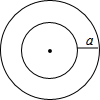 某圆环由圆心相同的两个圆组成,其示意图如图所示,两个圆的面积分别为251.2cm2和62.8cm2,则圆环的宽度a为($4\sqrt{5}-\sqrt{2}$)cm..(π=3.14,结果保留根号)
某圆环由圆心相同的两个圆组成,其示意图如图所示,两个圆的面积分别为251.2cm2和62.8cm2,则圆环的宽度a为($4\sqrt{5}-\sqrt{2}$)cm..(π=3.14,结果保留根号)