题目内容
8.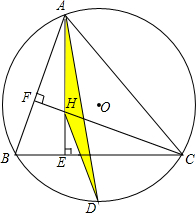 已知,△ABC内接于⊙O,∠BAC=60°,AE⊥BC,CF⊥AB.AE,CF相交于点H,点D为弧BC的中点,连接HD,AD.求证:△AHD为等腰三角形.
已知,△ABC内接于⊙O,∠BAC=60°,AE⊥BC,CF⊥AB.AE,CF相交于点H,点D为弧BC的中点,连接HD,AD.求证:△AHD为等腰三角形.
分析 连接AO、OD,过O作OM⊥AC,证出AM=AF,由AAS证得△AMO≌△AFH,得出AO=AH=OD,再证明AE∥OD,得出四边形OAHD为平行四边形,由AO=AH,得出四边形AHDO是菱形,即可得出结论.
解答 证明:连接AO、OD,过O作OM⊥AC,则AM=$\frac{1}{2}$AC,如图所示: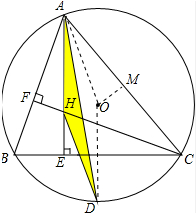
∵∠BAC=60°,CF⊥AB,
∴AF=$\frac{1}{2}$AC,
∴AM=AF,
∵AE⊥BC,CF⊥AB,
∴∠ABC+∠FHE=180°,
∵∠FHE+∠AHF=180°,
∴∠ABC=∠AHF,
∵∠AOM=$\frac{1}{2}$∠AOC=∠ABC,
∴∠AHF=∠AOM,
在△AMO与△AFH中,$\left\{\begin{array}{l}{∠AFH=∠AMO=90°}\\{∠AHF=∠AOM}\\{AF=AM}\end{array}\right.$,
∴△AMO≌△AFH(AAS),
∴AO=AH,
∵OD=OA,
∴AO=AH=OD,
∵点D为弧BC的中点,
∴OD⊥BC,
∵AE⊥BC,
∴AE∥OD,
∴四边形OAHD为平行四边形,
∵AO=AH,
∴四边形AHDO是菱形,
∴AH=HD,
∴△AHD为等腰三角形.
点评 本题考查了三角形外接圆与外心、垂径定理、全等三角形的判定与性质、含30°角直角三角形的性质、平行四边形的判定、菱形的判定与性质、等腰三角形的判定等知识,熟练掌握垂径定理与全等三角形的判定与性质以及菱形的判定与性质是解决问题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
18.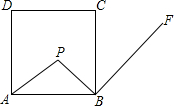 如图,点P是边长为5的正方形ABCD内一点,且PB=2,PB⊥BF,垂足为点B,请在射线BF上找一点M,使得以B,M,C为顶点的三角形与△ABP相似,则BM等于( )
如图,点P是边长为5的正方形ABCD内一点,且PB=2,PB⊥BF,垂足为点B,请在射线BF上找一点M,使得以B,M,C为顶点的三角形与△ABP相似,则BM等于( )
 如图,点P是边长为5的正方形ABCD内一点,且PB=2,PB⊥BF,垂足为点B,请在射线BF上找一点M,使得以B,M,C为顶点的三角形与△ABP相似,则BM等于( )
如图,点P是边长为5的正方形ABCD内一点,且PB=2,PB⊥BF,垂足为点B,请在射线BF上找一点M,使得以B,M,C为顶点的三角形与△ABP相似,则BM等于( )| A. | 2或$\frac{25}{2}$ | B. | 2 | C. | $\frac{25}{2}$ | D. | 2或$\frac{15}{2}$ |
19.计算$\frac{\sqrt{5}a}{\sqrt{10a}}$得到的最后结果是( )
| A. | $\frac{\sqrt{a}}{\sqrt{2}}$ | B. | $\frac{\sqrt{2a}}{2}$ | C. | $\sqrt{\frac{a}{2}}$ | D. | $\sqrt{\frac{2a}{2}}$ |
 已知:如图,正方形ABCD的边长为6,BM,DN分别平分正方形的两个外角,且满足∠MAN=45°,连接MC,NC,MN.
已知:如图,正方形ABCD的边长为6,BM,DN分别平分正方形的两个外角,且满足∠MAN=45°,连接MC,NC,MN.