题目内容
1.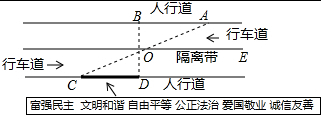 小明沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙0点,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息如下:如图,AB∥OE,OE∥CD,AC与BD相交于点O,OD⊥CD,垂足为点D,下列结论中不正确的是( )
小明沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙0点,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息如下:如图,AB∥OE,OE∥CD,AC与BD相交于点O,OD⊥CD,垂足为点D,下列结论中不正确的是( )| A. | ∠BOA=∠DOC | B. | AB∥CD | ||
| C. | ∠ABD=90° | D. | 与∠AOE相等的角共有2个 |
分析 根据对顶角相等,平行线的性质分别进行分析即可.
解答  解:A、∠BOA和∠DOC是对顶角,因此∠BOA=∠DOC正确,故此选项不合题意;
解:A、∠BOA和∠DOC是对顶角,因此∠BOA=∠DOC正确,故此选项不合题意;
B、∵AB∥OE,OE∥CD,
∴AB∥CD,正确,故此选项不合题意;
C、∵AB∥CD,
∴∠ABD=∠BDC,
∵OD⊥CD,
∴∠ADO=90°,
∴∠DBA=90°,正确,故此选项不合题意;
D、∵AB∥OE,
∴∠BAO=∠AOE,
∵CD∥EO,
∴∠OCD=∠AOE,
∵∠AOE=∠1,
∴与∠AOE相等的角有3个,原题说法错误,故此选项符合题意,
故选:D.
点评 此题主要考查了平行线的性质,关键是掌握两直线平行,同位角内错角相等.

练习册系列答案
相关题目
11.阅读下面材料,并解答其后的问题:
定义:两组领边分别相等的四边形叫做筝形.
如图1,四边形ABCD中,若AD=AB,CD=CB,则四边形ABCD是筝形.
类比研究:
我们在学完平行四边形后,知道可以从对称性、边、角和对角线四个角度对平行四边形的性质进行研究,请根据示例图形,完成下表:
(1)表格中①、②分别填写的内容是:
①轴对称图形;
②一条对角线垂直平分另一条对角线.
(2)演绎论证:证明筝形有关对角线的性质.
已知:在筝形ABCD中,AD=AB,BC=DC,AC、BD是对角线.
求证:AC垂直平分BD.
证明:
(3)运用:如图3,已知筝形ABCD中,AD=AB=4,CD=CB,∠A=90°,∠C=60°,求筝形ABCD的面积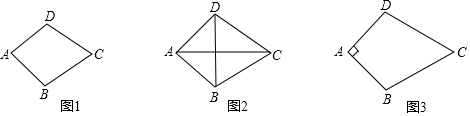
定义:两组领边分别相等的四边形叫做筝形.
如图1,四边形ABCD中,若AD=AB,CD=CB,则四边形ABCD是筝形.
类比研究:
我们在学完平行四边形后,知道可以从对称性、边、角和对角线四个角度对平行四边形的性质进行研究,请根据示例图形,完成下表:
| 四边形 | 示例图形 | 对称性 | 边 | 角 | 对角线 |
| 平行 四边形 |  | 两组对边分别平行,两组对边分别相等 | 两组对边分别平行,两组对边分别相等. | 两组对角 分别相等. | 对角线互相平分. |
| 等腰 梯形 | 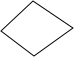 | ①轴对称图形 | 两组邻边分别相等 | 有一组对角相等 | ②一条对角线垂直平分另一条对角线 |
①轴对称图形;
②一条对角线垂直平分另一条对角线.
(2)演绎论证:证明筝形有关对角线的性质.
已知:在筝形ABCD中,AD=AB,BC=DC,AC、BD是对角线.
求证:AC垂直平分BD.
证明:
(3)运用:如图3,已知筝形ABCD中,AD=AB=4,CD=CB,∠A=90°,∠C=60°,求筝形ABCD的面积

 如图,方格是由边长为1个单位长度的正方形组成的.
如图,方格是由边长为1个单位长度的正方形组成的. 如图①所示是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
如图①所示是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.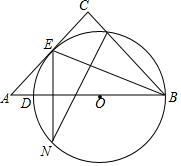 如图,在△ABC中,∠C=90°,D为AB边上一点,以DB为直径的⊙O与AC相切于点E,与BC相交于点F,FN⊥BE交⊙O于点N.
如图,在△ABC中,∠C=90°,D为AB边上一点,以DB为直径的⊙O与AC相切于点E,与BC相交于点F,FN⊥BE交⊙O于点N.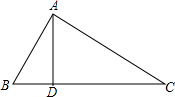 如图,在△ABC中,D是边BC上一点,若AB=10,BD=6,AD=8,AC=17,求BC的长.
如图,在△ABC中,D是边BC上一点,若AB=10,BD=6,AD=8,AC=17,求BC的长.