题目内容
6.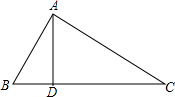 如图,在△ABC中,D是边BC上一点,若AB=10,BD=6,AD=8,AC=17,求BC的长.
如图,在△ABC中,D是边BC上一点,若AB=10,BD=6,AD=8,AC=17,求BC的长.
分析 在三角形ABD中,利用勾股定理的逆定理判断得到△ABD为直角三角形,即AD垂直于BC,在直角三角形ADC中,利用勾股定理求出DC的长,由BD+DC求出BC的长.
解答 解:在△ABD中,AB=10,BD=6,AD=8,
∴AB2=BD2+AD2,
∴△ABD为直角三角形,
∴AD⊥BC,即∠ADC=90°,
在Rt△ADC中,AD=8,AC=17,
根据勾股定理得:DC=$\sqrt{A{C}^{2}-A{D}^{2}}$=15,
∴BC=BD+CD=6+15=21.
点评 此题考查了勾股定理的逆定理,勾股定理,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
14.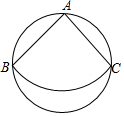 如图,从一块直径为24cm的圆形纸片上,剪出一个圆心角为90°的扇形ABC,使点A,B,C都在圆周上,将剪下的扇形围成一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
如图,从一块直径为24cm的圆形纸片上,剪出一个圆心角为90°的扇形ABC,使点A,B,C都在圆周上,将剪下的扇形围成一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
 如图,从一块直径为24cm的圆形纸片上,剪出一个圆心角为90°的扇形ABC,使点A,B,C都在圆周上,将剪下的扇形围成一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
如图,从一块直径为24cm的圆形纸片上,剪出一个圆心角为90°的扇形ABC,使点A,B,C都在圆周上,将剪下的扇形围成一个圆锥的侧面,则这个圆锥的底面圆的半径是( )| A. | 3$\sqrt{2}$cm | B. | 2$\sqrt{3}$cm | C. | 6cm | D. | 12cm |
1.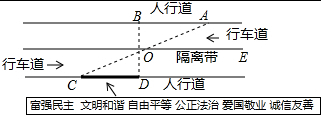 小明沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙0点,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息如下:如图,AB∥OE,OE∥CD,AC与BD相交于点O,OD⊥CD,垂足为点D,下列结论中不正确的是( )
小明沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙0点,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息如下:如图,AB∥OE,OE∥CD,AC与BD相交于点O,OD⊥CD,垂足为点D,下列结论中不正确的是( )
 小明沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙0点,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息如下:如图,AB∥OE,OE∥CD,AC与BD相交于点O,OD⊥CD,垂足为点D,下列结论中不正确的是( )
小明沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙0点,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息如下:如图,AB∥OE,OE∥CD,AC与BD相交于点O,OD⊥CD,垂足为点D,下列结论中不正确的是( )| A. | ∠BOA=∠DOC | B. | AB∥CD | ||
| C. | ∠ABD=90° | D. | 与∠AOE相等的角共有2个 |
15.计算(27a8)÷($\frac{1}{3}{a}^{3}$)÷(9a2)的顺序不正确的是( )
| A. | (27a8)÷[($\frac{1}{3}{a}^{3}$)÷(9a2)] | B. | [(27a8)÷($\frac{1}{3}{a}^{3}$)]÷(9a2) | C. | (27$÷\frac{1}{3}÷9$)a8-3-2 | D. | [(27a3)÷(9a2)]÷($\frac{1}{3}{a}^{3}$) |
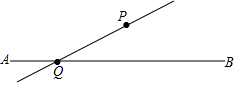 如图,按要求作图:
如图,按要求作图: