题目内容
16.计算:(1)$\frac{1}{2}\sqrt{12}$-(3$\sqrt{\frac{1}{3}}$+$\sqrt{5}}$)
(2)20170+$\sqrt{8}$+2×2-1-|$\sqrt{2}$-2|.
分析 (1)先把二次根式化为最简二次根式,然后合并即可;
(2)根据零指数幂、负整数指数的意义和绝对值的意义计算.
解答 解:(1)原式=$\sqrt{3}-\sqrt{3}-\sqrt{5}$
=$-\sqrt{5}$;
(2)原式=$1+2\sqrt{2}+1-2+\sqrt{2}$
=$3\sqrt{2}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.下列代数式书写规范的是( )
| A. | 1$\frac{1}{6}$a | B. | a×5 | C. | a÷b | D. | $\frac{1}{3}ab$ |
4.观察下表:
我们把某格中字母的和所得到的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y.回答下列问题:
(1)第2格的“特征多项式”为9x+4y,第3格的“特征多项式”为12x+6y;
(2)写出第5格的“特征多项式”与第6格的“特征多项式”,并求出第5格与第6格
“特征多项式”的差.
(3)试写出第n格的“特征多项式”.
| 序号 | 1 | 2 | 3 | … |
图形 | x x y x x y x x | x x x y y x x x y y x x x | x x x x y y y x x x x y y y x x x x | … |
(1)第2格的“特征多项式”为9x+4y,第3格的“特征多项式”为12x+6y;
(2)写出第5格的“特征多项式”与第6格的“特征多项式”,并求出第5格与第6格
“特征多项式”的差.
(3)试写出第n格的“特征多项式”.
1.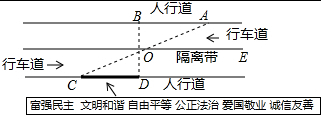 小明沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙0点,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息如下:如图,AB∥OE,OE∥CD,AC与BD相交于点O,OD⊥CD,垂足为点D,下列结论中不正确的是( )
小明沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙0点,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息如下:如图,AB∥OE,OE∥CD,AC与BD相交于点O,OD⊥CD,垂足为点D,下列结论中不正确的是( )
 小明沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙0点,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息如下:如图,AB∥OE,OE∥CD,AC与BD相交于点O,OD⊥CD,垂足为点D,下列结论中不正确的是( )
小明沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙0点,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息如下:如图,AB∥OE,OE∥CD,AC与BD相交于点O,OD⊥CD,垂足为点D,下列结论中不正确的是( )| A. | ∠BOA=∠DOC | B. | AB∥CD | ||
| C. | ∠ABD=90° | D. | 与∠AOE相等的角共有2个 |
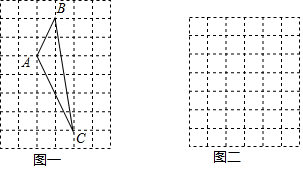
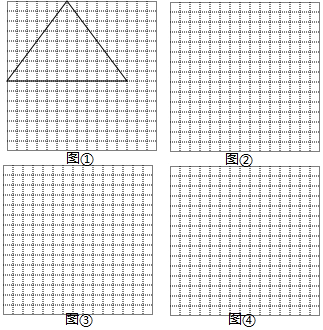 如图,在15×15的网格中,每个小正方形的边长均为1,每个小格的顶点叫做格点,图①中的三角形是以格点为顶点,边长都为整数的锐角三角形.
如图,在15×15的网格中,每个小正方形的边长均为1,每个小格的顶点叫做格点,图①中的三角形是以格点为顶点,边长都为整数的锐角三角形.
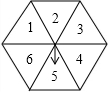 如图所示的是一个正六边形转盘被分成6个全等的等边三角形,指针位置固定,转动转盘后任其自由停止,其中的某个三角形会恰好停在指针所指的位置,并相应得到一个数 (指针指向两个三角形的公共边时,当作指向右边的三角形),这时称转动了转盘1次.
如图所示的是一个正六边形转盘被分成6个全等的等边三角形,指针位置固定,转动转盘后任其自由停止,其中的某个三角形会恰好停在指针所指的位置,并相应得到一个数 (指针指向两个三角形的公共边时,当作指向右边的三角形),这时称转动了转盘1次.