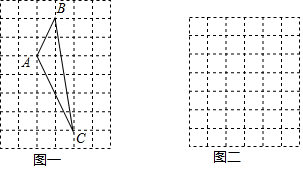
题目内容
9.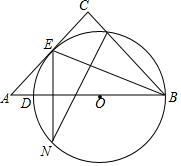 如图,在△ABC中,∠C=90°,D为AB边上一点,以DB为直径的⊙O与AC相切于点E,与BC相交于点F,FN⊥BE交⊙O于点N.
如图,在△ABC中,∠C=90°,D为AB边上一点,以DB为直径的⊙O与AC相切于点E,与BC相交于点F,FN⊥BE交⊙O于点N.(1)求证:BE平分∠ABC;
(2)若sinA=$\frac{2}{3}$,AB=30,求圆心O到EN的距离.
分析 (1)如图连接OE,根据切线的性质OE⊥AC,即可证得OE∥BC,进一步得到∠EBC=∠OBE,即可证得结论;
(2)解直角三角形求得BC=20,通过证得Rt△EBC≌Rt△EBF,得出BF=BC=20,设OF=h,则OB=20-h,OA=10+h,解直角三角形得到关于h的方程,解方程即可求得.
解答 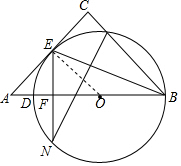 (1)证明:如图连接OE,
(1)证明:如图连接OE,
∵⊙O与AC相切于点E,
∴OE⊥AC,
∵∠C=90°,
∴OE∥BC,
∴∠OEB=∠EBC,
∵OE=OB,
∴∠OEB=∠OBE,
∴∠EBC=∠OBE,
∴BE平分∠ABC;
(2)解:设EN与AB的交点为F,
∵sinA=$\frac{2}{3}$,AB=30,
∴$\frac{BC}{AB}$=$\frac{2}{3}$,
∴BC=20,
∵BE平分∠ABC,OE⊥AC,∠C=90°,
∴EC=EF,
在Rt△EBC和Rt△EBF中
$\left\{\begin{array}{l}{EC=EF}\\{BE=BE}\end{array}\right.$
∴Rt△EBC≌Rt△EBF(HL),
∴BF=BC=20,
∴AF=30-20=10,
设OF=h,则OB=20-h,OA=10+h,
∵OE=OB,
∴OE=20-h,
∵sinA=$\frac{OE}{OA}$=$\frac{2}{3}$,
∴$\frac{20-h}{10+h}$=$\frac{2}{3}$,
解得h=8,
∴圆心O到EN的距离为8.
点评 本题考查了切线的性质、垂径定理以及解直角三角形的运用.作出辅助性构建等腰三角形设解题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
14.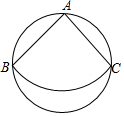 如图,从一块直径为24cm的圆形纸片上,剪出一个圆心角为90°的扇形ABC,使点A,B,C都在圆周上,将剪下的扇形围成一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
如图,从一块直径为24cm的圆形纸片上,剪出一个圆心角为90°的扇形ABC,使点A,B,C都在圆周上,将剪下的扇形围成一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
 如图,从一块直径为24cm的圆形纸片上,剪出一个圆心角为90°的扇形ABC,使点A,B,C都在圆周上,将剪下的扇形围成一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
如图,从一块直径为24cm的圆形纸片上,剪出一个圆心角为90°的扇形ABC,使点A,B,C都在圆周上,将剪下的扇形围成一个圆锥的侧面,则这个圆锥的底面圆的半径是( )| A. | 3$\sqrt{2}$cm | B. | 2$\sqrt{3}$cm | C. | 6cm | D. | 12cm |
1.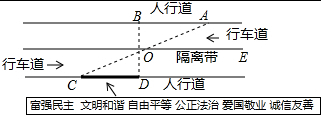 小明沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙0点,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息如下:如图,AB∥OE,OE∥CD,AC与BD相交于点O,OD⊥CD,垂足为点D,下列结论中不正确的是( )
小明沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙0点,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息如下:如图,AB∥OE,OE∥CD,AC与BD相交于点O,OD⊥CD,垂足为点D,下列结论中不正确的是( )
 小明沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙0点,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息如下:如图,AB∥OE,OE∥CD,AC与BD相交于点O,OD⊥CD,垂足为点D,下列结论中不正确的是( )
小明沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙0点,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息如下:如图,AB∥OE,OE∥CD,AC与BD相交于点O,OD⊥CD,垂足为点D,下列结论中不正确的是( )| A. | ∠BOA=∠DOC | B. | AB∥CD | ||
| C. | ∠ABD=90° | D. | 与∠AOE相等的角共有2个 |
 如图,在?ABCD中,AC⊥BC,过点D作DE∥AC交BC的延长线于点E,连接AE交CD于点F.
如图,在?ABCD中,AC⊥BC,过点D作DE∥AC交BC的延长线于点E,连接AE交CD于点F.