题目内容
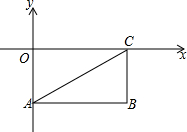 如图,矩形OABC的两边在坐标轴上,A(0,-2)、C(4,0),连接AC,若点P由点A出发以每秒1个单位的速度沿AB边向B移动,1秒以后点Q也由点A出发以每秒7个单位的速度沿AO、OC、CB边向点B移动,当其中一个点到达终点时,另一个点也停止移动,点P的移动时间为t秒.
如图,矩形OABC的两边在坐标轴上,A(0,-2)、C(4,0),连接AC,若点P由点A出发以每秒1个单位的速度沿AB边向B移动,1秒以后点Q也由点A出发以每秒7个单位的速度沿AO、OC、CB边向点B移动,当其中一个点到达终点时,另一个点也停止移动,点P的移动时间为t秒.(1)设△APQ的面积为y,求y与t的函数关系及定义域;
(2)当P到达AB中点时,求P、Q的坐标;
(3)在(2)的条件下,直线x=2上是否存在点H,使得∠HOQ>∠POQ?若存在,求点H的纵坐标的取值范围;若不存在,请说明理由.
考点:一次函数综合题
专题:
分析:(1)分类讨论点Q分别在OA,OC,BC上时,分别计算y的值,即可解题;
(2)根据P在AB中点,求得此时Q点的位置即可解题;
(3)分类讨论点Q分别在OA,OC,BC上时,分别计算y的取值范围,取交集,即可解题;
(2)根据P在AB中点,求得此时Q点的位置即可解题;
(3)分类讨论点Q分别在OA,OC,BC上时,分别计算y的取值范围,取交集,即可解题;
解答:解:(1)点Q运动
秒就停止,而此时P点仍未到达B点,
∴当1<t<
时,点Q在OA上,此时y=
AP•AQ=
×t×7(t-1)=
;
当
≤t≤
时,点Q在OC上,此时y=
AP•AO=t;
当
<t<
时,点Q在BC上,此时y=
AP•BQ=
;
(2)∵AB=4,
∴P到达AB中点耗时2秒,此时点Q走了1秒,位于BC中点,
∴此时点(2,-2),
点Q(4,-1);
(3)如图,画出直线x=2,在AB上标记P点,x=2上找到H点,

分类讨论:
①当点Q位于OA上时,∠HOQ>∠POQ,H纵坐标y>-2即可;
②当点Q位于OC上时,∠HOQ>∠POQ,H纵坐标y>2即可;
③当点Q位于BC上时,∠HOQ>∠POQ,H纵坐标y>2即可;
故存在,点H的纵坐标的取值范围为y>2.
| 8 |
| 7 |
∴当1<t<
| 9 |
| 7 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7t2-7t |
| 2 |
当
| 9 |
| 7 |
| 13 |
| 7 |
| 1 |
| 2 |
当
| 13 |
| 7 |
| 15 |
| 7 |
| 1 |
| 2 |
| 15t-7t2 |
| 2 |
(2)∵AB=4,
∴P到达AB中点耗时2秒,此时点Q走了1秒,位于BC中点,
∴此时点(2,-2),
点Q(4,-1);
(3)如图,画出直线x=2,在AB上标记P点,x=2上找到H点,

分类讨论:
①当点Q位于OA上时,∠HOQ>∠POQ,H纵坐标y>-2即可;
②当点Q位于OC上时,∠HOQ>∠POQ,H纵坐标y>2即可;
③当点Q位于BC上时,∠HOQ>∠POQ,H纵坐标y>2即可;
故存在,点H的纵坐标的取值范围为y>2.
点评:本题考查了一次函数的应用,考查了动点问题的分类讨论思维,本题中分类讨论Q点位置是解题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
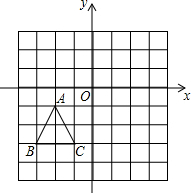 如图,已知△ABC三个顶点的坐标分别为A(-2,-1),B(-3,-3),C(-1,-3).
如图,已知△ABC三个顶点的坐标分别为A(-2,-1),B(-3,-3),C(-1,-3).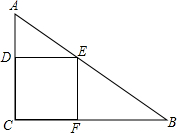 如图,在△ABC中,∠C=90°,CA=10cm,CB=15cm,求正方形CDEF的面积.
如图,在△ABC中,∠C=90°,CA=10cm,CB=15cm,求正方形CDEF的面积. 如图,等边△ABC中,延长AB至D,使BD=AB,延长AC至E,使CE=
如图,等边△ABC中,延长AB至D,使BD=AB,延长AC至E,使CE= 如图.大桥的圆拱的跨度CD为80米,拱高EF为20米,求这个圆拱所在圆的直径.
如图.大桥的圆拱的跨度CD为80米,拱高EF为20米,求这个圆拱所在圆的直径.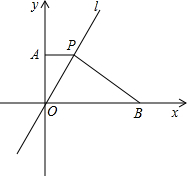 如图,在直角坐标系中,直线l经过原点O,点P是第一象限内直线l上的点,过点P作PA垂直y轴于点A,点P的横坐标为1,点B的横坐标为5,PB⊥PO,交x轴于点B.
如图,在直角坐标系中,直线l经过原点O,点P是第一象限内直线l上的点,过点P作PA垂直y轴于点A,点P的横坐标为1,点B的横坐标为5,PB⊥PO,交x轴于点B.