题目内容
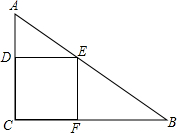如图，在△ABC中，∠C=90°，CA=10cm，CB=15cm，求正方形CDEF的面积．考点：相似三角形的判定与性质,正方形的性质
专题：
分析：设正方形的边长为x，则DE=CD=x，AD=10-x，利用平行线分线段成比例可得到关于x的方程，解得x再求其面积即可．
解答：解：
设正方形的边长为xcm，则DE=CD=xcm，AD=（10-x）cm，
∵DE∥BC，
∴
=
，即
=
，
解得x=6，
∴S正方形CDEF=x2=36（cm2）．
设正方形的边长为xcm，则DE=CD=xcm，AD=（10-x）cm，
∵DE∥BC，
∴
| DE |
| BC |
| AD |
| AC |
| x |
| 15 |
| 10-x |
| 10 |
解得x=6，
∴S正方形CDEF=x2=36（cm2）．
点评：本题主要考查平行线分线段成比例的性质，掌握平行线分线段所得线段对应成比例是解题的关键．
练习册系列答案
相关题目
如图，在Rt△ABC中，∠C=90°，DE⊥BC，BC=40，CD=10，DE=20，则AC的长为
如图所示，直线PD为△ABC一边BC的垂直平分线，点D为垂足，连接CP并延长CP交边AB于点F，射线BP交边AC于点E．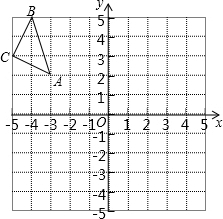
如图，在平面直角坐标系中，每个小正方形的边长为1，点A的坐标为（-3，2）．
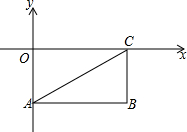如图，矩形OABC的两边在坐标轴上，A（0，-2）、C（4，0），连接AC，若点P由点A出发以每秒1个单位的速度沿AB边向B移动，1秒以后点Q也由点A出发以每秒7个单位的速度沿AO、OC、CB边向点B移动，当其中一个点到达终点时，另一个点也停止移动，点P的移动时间为t秒．