题目内容
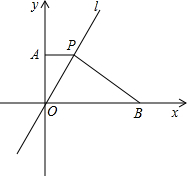 如图,在直角坐标系中,直线l经过原点O,点P是第一象限内直线l上的点,过点P作PA垂直y轴于点A,点P的横坐标为1,点B的横坐标为5,PB⊥PO,交x轴于点B.
如图,在直角坐标系中,直线l经过原点O,点P是第一象限内直线l上的点,过点P作PA垂直y轴于点A,点P的横坐标为1,点B的横坐标为5,PB⊥PO,交x轴于点B.(1)试说明PO2=PA•OB;
(2)点M为x轴上的动点,若有△AOM与△POB相似,求M的坐标.
考点:一次函数综合题
专题:
分析:(1)由条件证明△PAO∽△0PB,再利用相似三角形的性质可证得结论;
(2)由(1)结论可先求得PO,在Rt△PAO中求得AO,在Rt△POB中可求得PB,设M坐标为(x,0),可表示出MO,当△AOM与△POB相似分两种情况讨论,分别得到关于x的方程,解得x即可.
(2)由(1)结论可先求得PO,在Rt△PAO中求得AO,在Rt△POB中可求得PB,设M坐标为(x,0),可表示出MO,当△AOM与△POB相似分两种情况讨论,分别得到关于x的方程,解得x即可.
解答:解:(1)∵PA⊥y轴,
∴PA∥x轴,
∴∠APO=∠POB,
∵BP⊥PO,
∴∠PAO=∠OPB,
∴△PAO∽△OPB,
∴
=
,
∴PO2=PA•OB;
(2)∵P的横坐标为1,点B的横坐标为5,
∴PA=1,OB=5,
∴PO2=1×5=5,
∴PO=
,
在Rt△PAO中,由勾股定理可得AO=2,
在Rt△PBO中,由勾股定理可得PB=2
,
设M坐标为(x,0),则OM=|x|,
∵∠OPB=∠AOM=90°,
∴当△AOM与△POB相似时有两种情况,
①当△AOM∽△OPB时,则
=
,即
=
,解得x=±4,此时M坐标为(-4,0)或(4,0);
②当△AOM∽△BPO时,则
=
,即
=
,解得x=±1,此时M坐标为(-1,0)或(1,0);
综上可知点M坐标为(-4,0)或(4,0)或(-1,0)或(1,0).
∴PA∥x轴,
∴∠APO=∠POB,
∵BP⊥PO,
∴∠PAO=∠OPB,
∴△PAO∽△OPB,
∴
| PA |
| PO |
| PO |
| OB |
∴PO2=PA•OB;
(2)∵P的横坐标为1,点B的横坐标为5,
∴PA=1,OB=5,
∴PO2=1×5=5,
∴PO=
| 5 |
在Rt△PAO中,由勾股定理可得AO=2,
在Rt△PBO中,由勾股定理可得PB=2
| 5 |
设M坐标为(x,0),则OM=|x|,
∵∠OPB=∠AOM=90°,
∴当△AOM与△POB相似时有两种情况,
①当△AOM∽△OPB时,则
| AO |
| OP |
| OM |
| PB |
| 2 | ||
|
| |x| | ||
2
|
②当△AOM∽△BPO时,则
| AO |
| BP |
| OM |
| PO |
| 2 | ||
2
|
| |x| | ||
|
综上可知点M坐标为(-4,0)或(4,0)或(-1,0)或(1,0).
点评:本题主要考查相似三角形的判定和性质及勾股定理、点的坐标的意义等知识点的综合应用.掌握相似三角形的判定和性质是解题的关键,在(2)中注意分情况讨论和方程思想的应用.设出点的坐标表示出线段的长度,利用线段的关系得到关于x的方程是解决这类问题的一般思路.本题难度适中,考查基础知识.

练习册系列答案
相关题目
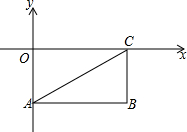 如图,矩形OABC的两边在坐标轴上,A(0,-2)、C(4,0),连接AC,若点P由点A出发以每秒1个单位的速度沿AB边向B移动,1秒以后点Q也由点A出发以每秒7个单位的速度沿AO、OC、CB边向点B移动,当其中一个点到达终点时,另一个点也停止移动,点P的移动时间为t秒.
如图,矩形OABC的两边在坐标轴上,A(0,-2)、C(4,0),连接AC,若点P由点A出发以每秒1个单位的速度沿AB边向B移动,1秒以后点Q也由点A出发以每秒7个单位的速度沿AO、OC、CB边向点B移动,当其中一个点到达终点时,另一个点也停止移动,点P的移动时间为t秒.