题目内容
 如图,等边△ABC中,延长AB至D,使BD=AB,延长AC至E,使CE=
如图,等边△ABC中,延长AB至D,使BD=AB,延长AC至E,使CE=| 1 |
| 2 |
考点:相似三角形的判定与性质
专题:证明题
分析:过点B作BM∥CD交AC于M,根据题意可知CF是△EBM的中位线,BM是△ACD的中位线,由三角形中位线定理可找到DF、CF和BM的关系,可证得结论.
解答: 证明:过点B作BM∥CD交AC于M,
证明:过点B作BM∥CD交AC于M,
∵BD=AB,
∴AM=CM
∴BM是△ACD的中位线,
∴DC=2BM,
∵CE=
AC,
∴CE=MC,
∴CF是△EMB的中位线,
∴BM=2CF,
∴DC=4CF,
∴DF=3CF.
 证明:过点B作BM∥CD交AC于M,
证明:过点B作BM∥CD交AC于M,∵BD=AB,
∴AM=CM
∴BM是△ACD的中位线,
∴DC=2BM,
∵CE=
| 1 |
| 2 |
∴CE=MC,
∴CF是△EMB的中位线,
∴BM=2CF,
∴DC=4CF,
∴DF=3CF.
点评:本题主要考查三角形中位线定理,利用条件构造三角形中位线,找到DC、FC和BM的关系是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,DE⊥BC,BC=40,CD=10,DE=20,则AC的长为
如图,在Rt△ABC中,∠C=90°,DE⊥BC,BC=40,CD=10,DE=20,则AC的长为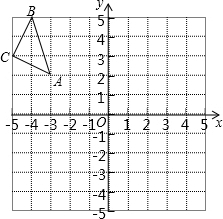 如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2).
如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2).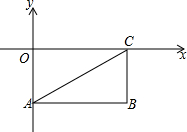 如图,矩形OABC的两边在坐标轴上,A(0,-2)、C(4,0),连接AC,若点P由点A出发以每秒1个单位的速度沿AB边向B移动,1秒以后点Q也由点A出发以每秒7个单位的速度沿AO、OC、CB边向点B移动,当其中一个点到达终点时,另一个点也停止移动,点P的移动时间为t秒.
如图,矩形OABC的两边在坐标轴上,A(0,-2)、C(4,0),连接AC,若点P由点A出发以每秒1个单位的速度沿AB边向B移动,1秒以后点Q也由点A出发以每秒7个单位的速度沿AO、OC、CB边向点B移动,当其中一个点到达终点时,另一个点也停止移动,点P的移动时间为t秒.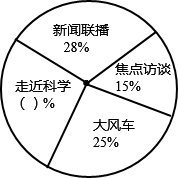 如图是某学校教师喜欢看的电视节目统计图.
如图是某学校教师喜欢看的电视节目统计图.