Question

5．已知AB是圆O的直径，点C，P在圆O上，PB=2$\sqrt{3}$，∠ABP=30°，PC=BC，则△PBC的面积为（　　）

• A． $\sqrt{3}$
• B． 2$\sqrt{3}$
• C． $\sqrt{3}$或3$\sqrt{3}$
• D． $\sqrt{3}$或4$\sqrt{3}$

Answer 1

分析 如图1，连接PA，过C作CD⊥PB于D，根据垂径定理得到PD=BD=$\sqrt{3}$，解直角三角形得到CD=1，于是得到△PBC的面积=$\frac{1}{2}$PB•CD=$\sqrt{3}$；如图2，连接PA，过C作CD⊥PB于D，根据等腰三角形的性质得到PD=BD=$\sqrt{3}$，解直角三角形得到CD=3，于是得到△PBC的面积=$\frac{1}{2}$PB•CD=3$\sqrt{3}$．

解答 解：如图1，
连接PA，过C作CD⊥PB于D，
∴PD=BD=$\sqrt{3}$，
∵AB是圆O的直径，
∴∠APB=90°，
∵∠ABP=30°，
∴∠A=60°，
∵PC=PB，
∴∠CPB=∠CBP=30°，
∴CD=1，
∴△PBC的面积=$\frac{1}{2}$PB•CD=$\sqrt{3}$；
如图2，连接PA，过C作CD⊥PB于D，
∵PC=PB，
∴PD=BD=$\sqrt{3}$，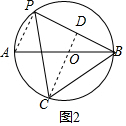
∵AB是圆O的直径，
∴∠APB=90°，
∵∠ABP=30°，
∴∠A=60°，
∴∠PCB=∠A=60°，
∴CD=3，
∴△PBC的面积=$\frac{1}{2}$PB•CD=3$\sqrt{3}$；
综上所述：△PBC的面积为$\sqrt{3}$或3$\sqrt{3}$，
故选C．

点评 本题考查了圆周角定理三角形的面积的计算，解直角三角形，正确的作出辅助线是解题的关键．