题目内容
5.某体育用品专卖店为了对某新品牌的羽毛球拍进行促销,推出两种优惠方案.方案一:买一支球拍赠送一打羽毛球;方案二,羽毛球x打(x≥20)供训练使用:按购买金额打九折付款,羽毛球每打售价10元,也可以两种方案混合购买.已知羽毛球拍每支售价60元,按哪种方案付款更合算.若专卖店允许以任意一种优惠方案购买.(1)写出每种优惠方案实际付款金额y(元)与 x(打)之间的函数关系式.
(2)比较购买同样多的羽毛球,校羽毛球队欲购买球拍20支,请就购买球拍20支和羽毛球50打设计一种最省钱的购买方法.
分析 (1)根据方案一、方案二的优惠政策列出函数关系式即可;
(2)因为允许可以任意选择一种优惠方案,也可以同时用两种方案购买,所以分三种情况分别讨论,进行比较即可.
解答 解:(1)方案一:y1=60×20+10(x-20)=10x+1000;
方案二:y2=(60×20+10x)×0.9=9x+1080.
(2)方案一:10×50+100=1600(元),
方案二:9×50+1080=1530(元),
两种方案买:20×60+(50-20)×10×0.9=1470(元),
∴用方案一买20支球拍,剩下的用方案二购买.
点评 本题考查了一次函数的应用,解决本题的关键是根据题意,列出函数解析式.注意的是方案的选择,一般要通过比较,选择最优的方案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.若a<b,则下列不等式中正确的是( )
| A. | a-3<b-3 | B. | a-b>0 | C. | $\frac{1}{3}a>\frac{1}{3}$b | D. | -2a<-2b |
14. 如图,正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )
如图,正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )
 如图,正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )
如图,正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )| A. | x<-2或x>2 | B. | x<-2或0<x<2 | C. | -2<x<0或0<x<2 | D. | -2<x<0或x>2 |
15.关于x的一元二次方程(m-2)x2+2x+1=0有实数根,则m的取值范围是( )
| A. | m≤3 | B. | m<3 | C. | m<3且m≠2 | D. | m≤3且m≠2 |
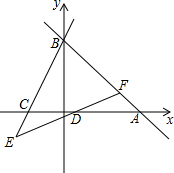 如图,直线y=-x+6与x轴交于点A,与y轴交于点B,C(-2,0),直线y=kx-k与x轴交于点D,交AB于F,交BC的延长线于E,若DE=DF,求k的值.
如图,直线y=-x+6与x轴交于点A,与y轴交于点B,C(-2,0),直线y=kx-k与x轴交于点D,交AB于F,交BC的延长线于E,若DE=DF,求k的值.
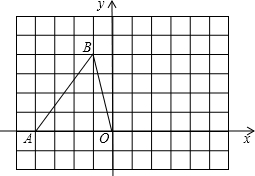 如图,在平面直角坐标系中,点A、B的坐标分别为A(-4,0),B(-1,4),将△AOB绕点O顺时针旋转90°
如图,在平面直角坐标系中,点A、B的坐标分别为A(-4,0),B(-1,4),将△AOB绕点O顺时针旋转90°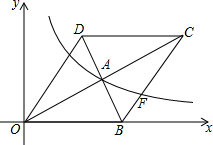 如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是(12,$\frac{8}{3}$).
如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是(12,$\frac{8}{3}$).