题目内容
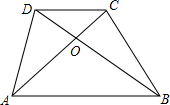如图，在四边形ABCD中，DC∥AB，AC与BD相交于点O，且| AO |
| CO |
| 3 |
| 2 |
考点：相似三角形的判定与性质
专题：常规题型
分析：根据平行线性质、三角形面积的计算和相似三角形面积比为边长比的平方可以解本题．
解答：解：过O作EF⊥AB，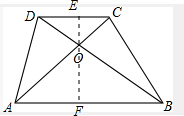
S△AOD：S△AOB：S△BOC：S△COD
S△AOD=S△ACD-S△COD；
S△BOC=S△BCD-S△COD；
S△AOD=S△BOC；
∵
=
，∴
=
=
，
S△COD：S△AOD=EO：（EF-EO）=EO：FO=2：3，
S△COD：S△AOB=4：9，
∴S△AOD：S△AOB：S△BOC：S△COD=6：9：6：4．
故答案为：6：9：6：4．
S△AOD：S△AOB：S△BOC：S△COD
S△AOD=S△ACD-S△COD；
S△BOC=S△BCD-S△COD；
S△AOD=S△BOC；
∵
| AO |
| CO |
| 3 |
| 2 |
| CD |
| AB |
| EO |
| FO |
| 2 |
| 3 |
S△COD：S△AOD=EO：（EF-EO）=EO：FO=2：3，
S△COD：S△AOB=4：9，
∴S△AOD：S△AOB：S△BOC：S△COD=6：9：6：4．
故答案为：6：9：6：4．
点评：本题考查了三角形面积的计算，考查了相似三角形面积比是边长比平方的性质．
练习册系列答案
相关题目
如图，直线AD，BC相交于点O，AB∥CD，AO：AD=2：5，若△AOB的周长为12，求△COD周长．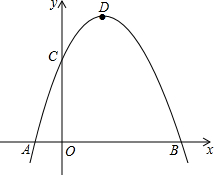
如图，抛物线y=-x2+2x+3与x轴相交于A，B两点（点A在点B的左侧），与y轴相交于点C，顶点为D．
如图所示，D、E分别是△ABC的边AC，AB上的点，∠ADE=∠B，AE=4，AC=16，则△ADE与△ACB的面积之比为