题目内容
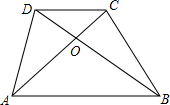
如图，直线AD，BC相交于点O，AB∥CD，AO：AD=2：5，若△AOB的周长为12，求△COD周长．考点：相似三角形的判定与性质
专题：常规题型
分析：因为周长的比等于相似比，所以根据AO：AD=2：5，可得AO：DO=2：3，可得△AOB的周长是△COD的周长为2：3，列等式计算即可．
解答：解：∵AB∥CD，
∴△AOB∽△DOC，
∵AO：AD=2：5，
∴AO：DO=2：3，
∴△COD的周长：△AOB的周长=3：2，
∵△AOB的周长为12cm，
∴△COD的周长是18cm．
∴△AOB∽△DOC，
∵AO：AD=2：5，
∴AO：DO=2：3，
∴△COD的周长：△AOB的周长=3：2，
∵△AOB的周长为12cm，
∴△COD的周长是18cm．
点评：此题主要考查学生对相似三角形（多边形）的周长的比等于相似比的运用．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
相关题目
如图，小宋作出了边长为2的第一个正方形A1B1C1D1，算出了它的面积．然后分别取正方形A1B1C1D1四边的中点A2、B2、C2、D2作出了第二个正方形A2B2C2D2，算出了它的面积．用同样的方法，作出了第三个正方形A3B3C3D3，算出了它的面积…，由此可得，第六个正方形A6B6C6D6的面积是（ ）A、4×(
| ||
B、4×(
| ||
C、4×(
| ||
D、4×(
|
一元二次方程x2-9=0的根是（ ）
| A、3 | B、±3 | C、9 | D、±9 |
一元二次方程（x+1）2=9可转化为两个一元一次方程，其中一个一元一次方程是x+1=3，则另一个一元二次方程是（ ）
| A、x-1=-3 |
| B、x-1=3 |
| C、x+1=3 |
| D、x+1=-3 |
如图，在四边形ABCD中，DC∥AB，AC与BD相交于点O，且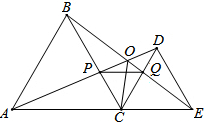
如图，△ABC、△CDE都是等边三角形，且点A、C、E在一条直线上，AD与BE、AD与BC、BE与CD分别交于点O、点P、点Q．求证：
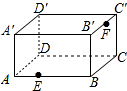如图是放在地面上的一个长方体盒子，其中AB=9，BB′=5，B′C′=6，在线段AB的三等分点E（靠近点A）处有一只蚂蚁，B′C′中点F处有一米粒，则蚂蚁沿长方体表面爬到米粒处的最短距离为（ ）