题目内容
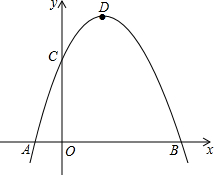 如图,抛物线y=-x2+2x+3与x轴相交于A,B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
如图,抛物线y=-x2+2x+3与x轴相交于A,B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.(1)直接写出A、B、C三点的坐标和抛物线的对称轴.
(2)连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.
①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形?
②△BCF的面积为S,求S与m的函数关系式,并求出S的最大值.
(3)现有一个以原点O为圆心,
| ||
| 4 |
考点:二次函数综合题
专题:
分析:(1)已知了抛物线的解析式,当y=0时可求出A,B两点的坐标,当x=0时,可求出C点的坐标.根据对称轴x=-
可得出对称轴的解析式.
(2)①PF的长就是当x=m时,抛物线的值与直线BC所在一次函数的值的差.可先根据B,C的坐标求出BC所在直线的解析式,然后将m分别代入直线BC和抛物线的解析式中,求得出两函数的值的差就是PF的长.根据直线BC的解析式,可得出E点的坐标,根据抛物线的解析式可求出D点的坐标,然后根据坐标系中两点的距离公式,可求出DE的长,然后让PF=DE,即可求出此时m的值.
②可将三角形BCF分成两部分来求:一部分是三角形PFC,以PF为底边,以P的横坐标为高即可得出三角形PFC的面积.一部分是三角形PFB,以PF为底边,以P、B两点的横坐标差的绝对值为高,即可求出三角形PFB的面积.然后根据三角形BCF的面积=三角形PFC的面积+三角形PFB的面积,可求出关于S、m的函数关系式,由此可求出S的最大值;
(3)设⊙O与直线AC相切于点E,连O′E,则O′E⊥AC,得到△ACO∽△O′CE,利用相似三角形的性质列出比例式即可求得x的值.
| b |
| 2a |
(2)①PF的长就是当x=m时,抛物线的值与直线BC所在一次函数的值的差.可先根据B,C的坐标求出BC所在直线的解析式,然后将m分别代入直线BC和抛物线的解析式中,求得出两函数的值的差就是PF的长.根据直线BC的解析式,可得出E点的坐标,根据抛物线的解析式可求出D点的坐标,然后根据坐标系中两点的距离公式,可求出DE的长,然后让PF=DE,即可求出此时m的值.
②可将三角形BCF分成两部分来求:一部分是三角形PFC,以PF为底边,以P的横坐标为高即可得出三角形PFC的面积.一部分是三角形PFB,以PF为底边,以P、B两点的横坐标差的绝对值为高,即可求出三角形PFB的面积.然后根据三角形BCF的面积=三角形PFC的面积+三角形PFB的面积,可求出关于S、m的函数关系式,由此可求出S的最大值;
(3)设⊙O与直线AC相切于点E,连O′E,则O′E⊥AC,得到△ACO∽△O′CE,利用相似三角形的性质列出比例式即可求得x的值.
解答:解:(1)设0=-x2+2x+3,
解得:x=-1或3,
∵抛物线y=-x2+2x+3与x相交于AB(点A点B左侧),
∴A(-1,0),B(3,0),
∵抛物线与y轴相交于点C,
∴C(0,3),
∴抛物线的对称轴是:直线x=1.
(2)①设直线BC的函数关系式为y=kx+b,把B(3,0),C(0,3)分别代入,
得
,解得:k=-1,b=3
∴直线BC的函数关系式为y=-x+3.
当x=1时,y=-1+3=2,∴E(1.2).
当x=m时,y=-m+3,∴P(m,-m+3)
在y=-x2+2x+3中,当x=1时,y=4,∴D(1,4).
当x=m时,y=-m2+2m+3,
∴F(m,-m2+2m+3),
∴线段DE=4-2=2,
线段PF=-m2+2m+3-(-m+3)=-m2+3m,
∵PF∥DE
∴当PF=DE时,四边形PEDF为平行四边形.
由-m2+3m=2,解得m=2或m=1(不合题意,舍去).
因此,当m=2时,四边形PEDF为平行四边形.
②设直线PF与x轴交于点M,由B(3,0),O(0,0),可得OB=OM+MB=3.
∵S=S△EPF+S△CPF,
即S=
PF•BM+
PF•OM
=
PF(BM+OM)
=
PF•OB,
∴S=
×3(-m2+3m)=-
m2+
m(0≤m≤3)
∴当m=-
=
时
S最大值=
;
(3)如图,设⊙O与直线AC相切于点E,连O′E,则O′E⊥AC,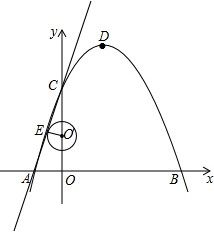
∵AO⊥CO,
∴∠O′EC=∠COA=90°
∵∠ACO=∠ECO,
∴△ACO∽△O′CE,
∴
=
,
由(1)得AO=1,CO=3,AC=
,
设x秒后⊙0与AC相切,
则OO′=x,CO′=|3-x|,
∴
=
,
解得:x=0.5或5.5,
∴0.5或5.5秒后⊙O与直线AC相切.
解得:x=-1或3,
∵抛物线y=-x2+2x+3与x相交于AB(点A点B左侧),
∴A(-1,0),B(3,0),
∵抛物线与y轴相交于点C,
∴C(0,3),
∴抛物线的对称轴是:直线x=1.
(2)①设直线BC的函数关系式为y=kx+b,把B(3,0),C(0,3)分别代入,
得
|
∴直线BC的函数关系式为y=-x+3.
当x=1时,y=-1+3=2,∴E(1.2).
当x=m时,y=-m+3,∴P(m,-m+3)
在y=-x2+2x+3中,当x=1时,y=4,∴D(1,4).
当x=m时,y=-m2+2m+3,
∴F(m,-m2+2m+3),
∴线段DE=4-2=2,
线段PF=-m2+2m+3-(-m+3)=-m2+3m,
∵PF∥DE
∴当PF=DE时,四边形PEDF为平行四边形.
由-m2+3m=2,解得m=2或m=1(不合题意,舍去).
因此,当m=2时,四边形PEDF为平行四边形.
②设直线PF与x轴交于点M,由B(3,0),O(0,0),可得OB=OM+MB=3.
∵S=S△EPF+S△CPF,
即S=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
∴S=
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
∴当m=-
| ||
2×(-
|
| 3 |
| 2 |
S最大值=
| 27 |
| 8 |
(3)如图,设⊙O与直线AC相切于点E,连O′E,则O′E⊥AC,

∵AO⊥CO,
∴∠O′EC=∠COA=90°
∵∠ACO=∠ECO,
∴△ACO∽△O′CE,
∴
| AC |
| OC |
| OA |
| OE |
由(1)得AO=1,CO=3,AC=
| 10 |
设x秒后⊙0与AC相切,
则OO′=x,CO′=|3-x|,
∴
| ||
| |3-x| |
| 1 | ||||
|
解得:x=0.5或5.5,
∴0.5或5.5秒后⊙O与直线AC相切.
点评:本题主要考查了二次函数的综合应用,根据二次函数得出相关点的坐标和对称轴的解析式是解题的基础,其中用到的知识点有平行四边形的判定和性质、解一元二次方程、用待定系数法确定一次函数的解析式,三角形面积公式的运用.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
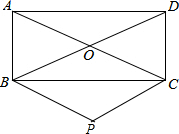 如图,在矩形ABCD中,对角线AC与DB相交于点O,过点C作CP∥DB,过点B作BP∥AC,两线相交于点P.求证:四边形COBP是菱形.
如图,在矩形ABCD中,对角线AC与DB相交于点O,过点C作CP∥DB,过点B作BP∥AC,两线相交于点P.求证:四边形COBP是菱形.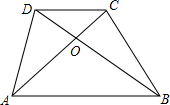 如图,在四边形ABCD中,DC∥AB,AC与BD相交于点O,且
如图,在四边形ABCD中,DC∥AB,AC与BD相交于点O,且 在△ABC中,∠ACB=90°,CD是高.CA:CB=m:n,求证:AD:DB=m2:n2.
在△ABC中,∠ACB=90°,CD是高.CA:CB=m:n,求证:AD:DB=m2:n2.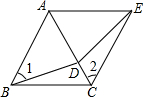 已知:如图所示,D在等边△ABC的边AC上,∠ACE=∠ABD,CE=BD.试说明:
已知:如图所示,D在等边△ABC的边AC上,∠ACE=∠ABD,CE=BD.试说明: 如图,点P是等边△ABC内的一点,分别连接PA、PB、PC,以BP为边作∠PBQ=60°,且BQ=BP,连接PQ、QC.
如图,点P是等边△ABC内的一点,分别连接PA、PB、PC,以BP为边作∠PBQ=60°,且BQ=BP,连接PQ、QC.