题目内容
直角三角形两直角边的比是5:12,斜边上的中线为13cm,则两条直角边分别为多少?
考点:勾股定理,直角三角形斜边上的中线
专题:
分析:根据“直角三角形斜边上的中线等于斜边的一半”求得该直角三角形的斜边长为26cm.再根据勾股定理来求两条直角边.
解答:解:∵一个直角三角形斜边上的中线为13cm,
∴斜边长为2×13=26(cm).
设一条直角边长为5xcm,则另一条直角边长为12xcm,
根据勾股定理知,
(5x)2+(12x)2=262,
解得x=±2(负值舍去),
5x=5×2=10,
12x=12×2=24.
故两条直角边分别为10cm,24cm.
∴斜边长为2×13=26(cm).
设一条直角边长为5xcm,则另一条直角边长为12xcm,
根据勾股定理知,
(5x)2+(12x)2=262,
解得x=±2(负值舍去),
5x=5×2=10,
12x=12×2=24.
故两条直角边分别为10cm,24cm.
点评:本题考查了直角三角形斜边上的中线,勾股定理.直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
相关题目
一元二次方程x2-9=0的根是( )
| A、3 | B、±3 | C、9 | D、±9 |
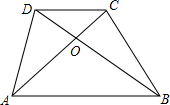 如图,在四边形ABCD中,DC∥AB,AC与BD相交于点O,且
如图,在四边形ABCD中,DC∥AB,AC与BD相交于点O,且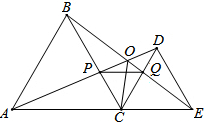 如图,△ABC、△CDE都是等边三角形,且点A、C、E在一条直线上,AD与BE、AD与BC、BE与CD分别交于点O、点P、点Q.求证:
如图,△ABC、△CDE都是等边三角形,且点A、C、E在一条直线上,AD与BE、AD与BC、BE与CD分别交于点O、点P、点Q.求证: