题目内容
 在平行四边形ABCD中,AE⊥BC于E,CF⊥AD于F,AE交BF于M,CF交DE于N.
在平行四边形ABCD中,AE⊥BC于E,CF⊥AD于F,AE交BF于M,CF交DE于N.(1)求证:MENF为平行四边形;
(2)若∠ANE=∠ABC,AB=4,AD=3
| 3 |
考点:平行四边形的判定与性质,相似三角形的判定与性质
专题:
分析:(1)由平行四边形的性质结合条件可证明四边形AECF和四边形BEDF为平行四边形,可分别得到AE∥CF,BF∥DE,可证明四边形MENF为平行四边形;
(2)由条件可证明△ADN∽△DEC,利用相似三角形的性质可求得AN.
(2)由条件可证明△ADN∽△DEC,利用相似三角形的性质可求得AN.
解答:(1)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
∵AE⊥BC,CF⊥AD,
∴∠AEC=∠CFA=90°,
∴∠AEC+∠EAF=∠EAF+∠AFC=180°,
∴AE∥CF,
∴四边形AECF为平行四边形,
∴AF=CE,
∴BE=DF,且BE∥DF,
∴四边形BEDF为平行四边形,
∴BF∥DE,
∴四边形MENF为平行四边形;
(2)解:∵四边形ABCD为平行四边形,
∴∠ABC+∠ECD=180°,
而∠ANE=∠ABC,
∴∠AND=∠DCE,
又∵AD∥BC,
∴∠ADN=∠DEC,
∴△ADN∽△DEC,
∴
=
,
∴AN=
=
=2
.
∴AD∥BC,AD=BC,
∵AE⊥BC,CF⊥AD,
∴∠AEC=∠CFA=90°,
∴∠AEC+∠EAF=∠EAF+∠AFC=180°,
∴AE∥CF,
∴四边形AECF为平行四边形,
∴AF=CE,
∴BE=DF,且BE∥DF,
∴四边形BEDF为平行四边形,
∴BF∥DE,
∴四边形MENF为平行四边形;
(2)解:∵四边形ABCD为平行四边形,
∴∠ABC+∠ECD=180°,
而∠ANE=∠ABC,
∴∠AND=∠DCE,
又∵AD∥BC,
∴∠ADN=∠DEC,
∴△ADN∽△DEC,
∴
| AD |
| DE |
| AN |
| CD |
∴AN=
| AD•CD |
| DE |
3
| ||
| 6 |
| 3 |
点评:本题主要考查平行四边形的性质和判定,掌握平行四边形的性质和判定是解题的关键,即①两组对边分别平行的四边形?平行四边形,②两组对边分别相等的四边形?平行四边形,③一组对边分别平行且相等的四边形?平行四边形,④两组对角分别相等的四边形?平行四边形,⑤对角线互相平分的四边形?平行四边形.

练习册系列答案
相关题目
 已知:如图,∠1=∠2,∠C=∠D,请由此找出所有互相平行的直线,并说明理由.
已知:如图,∠1=∠2,∠C=∠D,请由此找出所有互相平行的直线,并说明理由. 如图,大长方形ABCD被分为四个小长方形,其中小长方形AEMF、FMGD、MHCG的面积分别为3、2、4,则△EHD的面积为
如图,大长方形ABCD被分为四个小长方形,其中小长方形AEMF、FMGD、MHCG的面积分别为3、2、4,则△EHD的面积为 如图,BC=2,AC=
如图,BC=2,AC= 如图,P为等腰三角形ABC的底边AB上的任意一点,PE⊥AC于点E,PF⊥BC于点F,AD⊥BC于点D.求证:PE+PF=AD.
如图,P为等腰三角形ABC的底边AB上的任意一点,PE⊥AC于点E,PF⊥BC于点F,AD⊥BC于点D.求证:PE+PF=AD.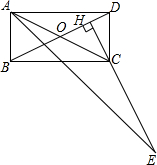 如图,在矩形ABCD中,点H在对角线BD上.HC⊥BD,HC的延长线交∠BAD的平分线于点E.求证:CE=BD.
如图,在矩形ABCD中,点H在对角线BD上.HC⊥BD,HC的延长线交∠BAD的平分线于点E.求证:CE=BD. 如图,学校位于高速路AB的一侧(AB成一直线),点A、点B为高速路上距学校直线距离最近的2个隧道出入口,点C、点D为学校的两幢教学楼.经测量,∠ACB=90°,∠ADB>90°,AC=600m,AB=1000m,D到高速路的最短直线距离DE=400m.
如图,学校位于高速路AB的一侧(AB成一直线),点A、点B为高速路上距学校直线距离最近的2个隧道出入口,点C、点D为学校的两幢教学楼.经测量,∠ACB=90°,∠ADB>90°,AC=600m,AB=1000m,D到高速路的最短直线距离DE=400m. 如图,OA⊥BC于点O,OD平分∠AOB,OE平分∠DOC,求∠DOE的度数.
如图,OA⊥BC于点O,OD平分∠AOB,OE平分∠DOC,求∠DOE的度数. 四边形ABCD是正方形,圆心角等于90°,OE=OF=10,问:正方形边长多少?
四边形ABCD是正方形,圆心角等于90°,OE=OF=10,问:正方形边长多少?