Question

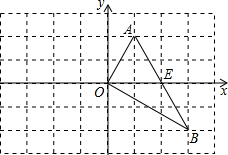已知在坐标系中的△AOB，顶点A（1，2）、B（3，-2），边AB与x轴交于点E．
（1）画出△AOB关于y轴对称的△A′OB′，并写出△A′OB′的顶点坐标；
（2）求以直线AB为图象的一次函数解析式，说明：E（2，0）和OA=AE成立理由；
（3）求△AOB的面积．

Answer 1

考点：作图-轴对称变换,待定系数法求一次函数解析式

专题：作图题

分析：（1）根据网格结构找出点A′、B′的位置，然后与点O顺次连接即可；
（2）设直线AB的解析式为y=kx+b，然后利用待定系数法求一次函数解析式解答；求出直线与x轴的交点即为E，过点A作AD⊥x轴于D，求出点D的坐标，从而得到OD=DE，然后根据线段垂直平分线上的点到两端点的距离相等证明即可；
（3）根据S_△AOB=S_△AOE+S_△BOE列式计算即可得解．

解答：解：（1）△A′OB′如图所示，A′（-1，2），O（0，0），B′（-3，-2）；

（2）设直线AB的解析式为y=kx+b，
代入A（1，2），B（3，-2）得，

k+b=2 3k+b=-2

，
解得

k=-2 b=4

，
所以，直线AB的解析式为y=-2x+4，
直线AB与x轴相交时，y=0，则-2x+4=0，
解得x=2，
所以E（2，0）为AB与x轴的交点；
过点A作AD⊥x轴于D，显然D（1，0），
∴OD=DE=1，
∴AD垂直平分OE，
∴OA=AE；

（3）S_△AOB=S_△AOE+S_△BOE，
=

1

2

×2×2+

1

2

×2×2，
=2+2，
=4．

点评：本题考查了利用轴对称变换作图，待定系数法求一次函数解析式，线段垂直平分线上的点到两端点的距离相等的性质，三角形的面积，难点在于（3）把一个三角形的面积分成两个三角形的面积的和求解．