题目内容
 以A、B、C为圆心的三个圆,半径均为r,其中1<r<2,每两个圆心间的距离都是2.若B′是⊙A和⊙C的交点且在⊙B外,C′是⊙A和⊙B的交点且在⊙C外,试求B′C′的长.
以A、B、C为圆心的三个圆,半径均为r,其中1<r<2,每两个圆心间的距离都是2.若B′是⊙A和⊙C的交点且在⊙B外,C′是⊙A和⊙B的交点且在⊙C外,试求B′C′的长.考点:圆与圆的位置关系
专题:
分析:由“圆心间的距离都是2”易知三角形ABC为边为2的正三角形,AB′C是腰为r、底为2的等腰三角形,其高B′F=
=
,根据三角形全等判定出C′B′∥BC,根据相似性易证△B′FE∽△BCF相似求得:EB′=
,EF=
,△ADE是等边三角形,DE=AE=1-
由C′D=EB′,得出B′C′=2EB′+DE=
+1-
=
+1.
| B′C2-FC2 |
| r2-1 |
2
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
4
| ||
| 3 |
| ||
| 3 |
| 3r2-3 |
解答:
解:如图,连接AC,BC,AB,AC′AB′BC′,AC交B′C′于点E,AB交B′C′于点D,作B′F⊥AC交AC于点F,
∵每两个圆心间的距离都是2.
∴△ABC为边长为2的正三角形,
∵△AB′C是等腰三角形且AB′=CB′=r,
∴B′F=
=
,
∵A、B、C为圆心的三个圆,半径均为r,每两个圆心间的距离都是2,
∴在△AC′B和△AB′C中,
,
∴△AC′B≌△AB′C(SSS),
∴∠AC′B=∠AB′C,∠C′BA=∠B′CA,
∵∠AC′B′=∠AB′C′,∠ABC=∠ACB,
∴∠BC′B′=∠CB′C′,∠C′BC=∠B′CB,
∴∠B′C′B+∠C′BC=180°,
∴C′B′∥BC,
又∵B,F,B′在同一条直线上,
∴∠C′B′B=∠B′BC,∠B′EC=∠BCE,
∴△B′FE∽△BCF
∴
=
,
=
,
∵B′F=
,BF=
,FC=1,BC=2,
∴EB′=
,EF=
,
∴AE=1-EF=1-
∵△ADE是等边三角形,
∴DE=AE=1-
∵C′D=EB′
∴B′C′=2EB′+DE=
+1-
=
+1

解:如图,连接AC,BC,AB,AC′AB′BC′,AC交B′C′于点E,AB交B′C′于点D,作B′F⊥AC交AC于点F,
∵每两个圆心间的距离都是2.
∴△ABC为边长为2的正三角形,
∵△AB′C是等腰三角形且AB′=CB′=r,
∴B′F=
| B′C2-FC2 |
| r2-1 |
∵A、B、C为圆心的三个圆,半径均为r,每两个圆心间的距离都是2,
∴在△AC′B和△AB′C中,
|
∴△AC′B≌△AB′C(SSS),
∴∠AC′B=∠AB′C,∠C′BA=∠B′CA,
∵∠AC′B′=∠AB′C′,∠ABC=∠ACB,
∴∠BC′B′=∠CB′C′,∠C′BC=∠B′CB,
∴∠B′C′B+∠C′BC=180°,
∴C′B′∥BC,
又∵B,F,B′在同一条直线上,
∴∠C′B′B=∠B′BC,∠B′EC=∠BCE,
∴△B′FE∽△BCF
∴
| B′F |
| BF |
| EB′ |
| BC |
| B′F |
| BF |
| EF |
| FC |
∵B′F=
| r2-1 |
| 3 |
∴EB′=
2
| ||
| 3 |
| ||
| 3 |
∴AE=1-EF=1-
| ||
| 3 |
∵△ADE是等边三角形,
∴DE=AE=1-
| ||
| 3 |
∵C′D=EB′
∴B′C′=2EB′+DE=
4
| ||
| 3 |
| ||
| 3 |
| 3r2-3 |
点评:本题主要考查了圆与圆的位置关系,解题的关键是求出C′B′∥BC,再利用相似三角形求线段的长度.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 如图,在等腰梯形ABCD中,AD∥AB,若∠B+∠C=90°,AD=AB=2,则底边BC的长为( )
如图,在等腰梯形ABCD中,AD∥AB,若∠B+∠C=90°,AD=AB=2,则底边BC的长为( )| A、3 | ||
| B、4 | ||
C、2+2
| ||
D、2+
|
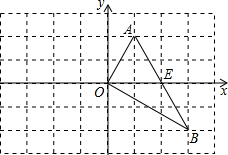 已知在坐标系中的△AOB,顶点A(1,2)、B(3,-2),边AB与x轴交于点E.
已知在坐标系中的△AOB,顶点A(1,2)、B(3,-2),边AB与x轴交于点E. 如图,菱形ABCD中,∠BCD=120°,点F是BD上一点,EF⊥CF,AE⊥EF,AE=3,EF=4,求AB长.
如图,菱形ABCD中,∠BCD=120°,点F是BD上一点,EF⊥CF,AE⊥EF,AE=3,EF=4,求AB长.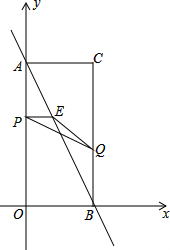 如图,在平面直角坐标系中,已知矩形AOBC的顶点C的坐标是(2,4),动点P从点A出发,沿线段AO向终点O运动,同时动点Q从点B出发,沿线段BC向终点C运动.点P、Q的运动速度均为1个单位,运动时间为t秒.过点P作PE⊥AO交AB于点E.
如图,在平面直角坐标系中,已知矩形AOBC的顶点C的坐标是(2,4),动点P从点A出发,沿线段AO向终点O运动,同时动点Q从点B出发,沿线段BC向终点C运动.点P、Q的运动速度均为1个单位,运动时间为t秒.过点P作PE⊥AO交AB于点E. 如图,在平行四边形ABCD中,∠A+∠C=160°,求∠A,∠B,∠C,∠D的度数.
如图,在平行四边形ABCD中,∠A+∠C=160°,求∠A,∠B,∠C,∠D的度数.