题目内容
 如图,将矩形ABCD绕点C沿顺时针方向旋转90°到矩形A′B′CD′的位置,AB=2,AD=4,则阴影部分的面积为
如图,将矩形ABCD绕点C沿顺时针方向旋转90°到矩形A′B′CD′的位置,AB=2,AD=4,则阴影部分的面积为考点:扇形面积的计算,旋转的性质
专题:
分析:先求出CE=2CD,求出∠DEC=30°,求出∠DCE=60°,DE=2
,分别求出扇形CEB′和三角形CDE的面积,即可求出答案.
| 3 |
解答:解:∵四边形ABCD是矩形,
∴AD=BC=4,CD=AB=2,∠BCD=∠ADC=90°,
∴CE=BC=4,
∴CE=2CD,
∴∠DEC=30°,
∴∠DCE=60°,
由勾股定理得:DE=2
,
∴阴影部分的面积是S=S扇形CEB′-S△CDE=
-
×2×2
=
π-2
,
故答案为:
π-2
.
∴AD=BC=4,CD=AB=2,∠BCD=∠ADC=90°,
∴CE=BC=4,
∴CE=2CD,
∴∠DEC=30°,
∴∠DCE=60°,
由勾股定理得:DE=2
| 3 |
∴阴影部分的面积是S=S扇形CEB′-S△CDE=
| 60π×42 |
| 360 |
| 1 |
| 2 |
| 3 |
| 8 |
| 3 |
| 3 |
故答案为:
| 8 |
| 3 |
| 3 |
点评:本题考查了扇形的面积,勾股定理,直角三角形的性质的应用,解此题的关键是能正确求出扇形CEB′和三角形CDE的面积,题目比较好,难度适中.

练习册系列答案
相关题目
函数y=
+(x-1)-2中自变量x的取值范围是( )
| 2-x |
| A、x≤2 |
| B、x≠1 |
| C、x<2且x≠1 |
| D、x≤2且x≠1 |
 如图,在等腰梯形ABCD中,AD∥AB,若∠B+∠C=90°,AD=AB=2,则底边BC的长为( )
如图,在等腰梯形ABCD中,AD∥AB,若∠B+∠C=90°,AD=AB=2,则底边BC的长为( )| A、3 | ||
| B、4 | ||
C、2+2
| ||
D、2+
|
 如图,∠1=∠2,∠C=∠D,那么∠A=∠F,为什么?
如图,∠1=∠2,∠C=∠D,那么∠A=∠F,为什么? 如图,△ABC绕顶点A逆时针旋转30°至△ADE,∠B=40°,∠DAC=50°,则∠E=
如图,△ABC绕顶点A逆时针旋转30°至△ADE,∠B=40°,∠DAC=50°,则∠E=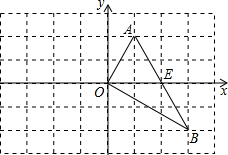 已知在坐标系中的△AOB,顶点A(1,2)、B(3,-2),边AB与x轴交于点E.
已知在坐标系中的△AOB,顶点A(1,2)、B(3,-2),边AB与x轴交于点E.