题目内容
17. 如图,延长平行四边形ABCD的边DC到E,使CE=CD,连结AE交BC于点F.
如图,延长平行四边形ABCD的边DC到E,使CE=CD,连结AE交BC于点F.(1)试说明:△ABF≌△ECF;
(2)连结AC,BD相交于O,连结OF,问OF与AB有怎样的数量关系与位置关系,说明理由;
(3)若AE=AD,连接BE,四边形ABEC是什么特殊四边形,说明理由;
(4)在(3)的条件下,当△ABC满足AB=AC条件时,四边形ABEC是正方形.
分析 (1)利用平行四边形的性质得出∠ABF=∠ECF,∠BAF=∠CEF,进而利用全等三角形的判定得出即可;
(2)根据题意可判断出OF是△ABC的中位线,从而可判断出数量及位置关系;
(3)首先判定四边形ABEC是平行四边形,进而利用矩形的判定定理得出即可;
(4)根据邻边相等的矩形是正方形即可得出结论.
解答  证明:(1)∵四边形ABCD是平行四边形,
证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠ABF=∠ECF,∠BAF=∠CEF,
又∵CE=DC,
∴AB=CE.
在△ABF和△ECF中,
∵$\left\{\begin{array}{l}ABF=∠ECF\\ AB=CE\\∠BAF=∠CEF\end{array}\right.$,
∴△ABF≌△ECF(ASA);
(2)OF=$\frac{1}{2}$AB,OF∥AB.
证明:∵OA=OC,BF=FC,
∴OF是△ABC的中位线.
∴OF=$\frac{1}{2}$AB,OF∥AB;
(3)连接BE,
∵AB∥CD,AB=CE,
∴四边形ABEC是平行四边形,
又∵AE=AD,
∴AC⊥DE,即∠ACE=90°,
∴平行四边形ABEC是矩形;
(4)∵由(3)知,四边形ABEC是矩形,
∴AC=AB时,四边形ABEC是正方形.
故答案为:AB=AC.
点评 此题考查的是四边形综合题,涉及到平行四边形的性质、全等三角形的判定及性质,矩形的判定与性质,难度一般,解答本题的关键是根据题意得出OF是△ABC的中位线.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
9.(-8)2的立方根是( )
| A. | -2 | B. | ±2 | C. | 4 | D. | ±4 |
6.已知数据$\sqrt{3}$,$\frac{1}{3}$,$\sqrt{2}$,π,-3.14,其中无理数出现的频率为( )
| A. | 80% | B. | 60% | C. | 40% | D. | 20% |
 如图,学校打算用长为16cm的篱笆围成一个长方形的生物园饲养小兔,生物园一面靠墙(篱笆只需围三面,AB为宽);
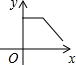
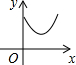
如图,学校打算用长为16cm的篱笆围成一个长方形的生物园饲养小兔,生物园一面靠墙(篱笆只需围三面,AB为宽);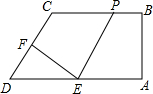 如图,在四边形ABCD中,BC∥AD,∠A=90°,BC<AD,E为AD的中点,F为CD的中点,P是一动点,从点A开始沿AB-BC匀速运动,到达点C即止,记点P运动的时间为x,四边形PEFC的面积为y,y与x关系所反映的图象可能是( )
如图,在四边形ABCD中,BC∥AD,∠A=90°,BC<AD,E为AD的中点,F为CD的中点,P是一动点,从点A开始沿AB-BC匀速运动,到达点C即止,记点P运动的时间为x,四边形PEFC的面积为y,y与x关系所反映的图象可能是( )

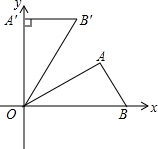 如图,在平面直角坐标系中,Rt△OAB的斜边OB在x轴的正半轴上,点A在第一象限,将△OAB,使点O按逆时针方向旋转至△OA′B′,使点A的对应点A′落在y轴的正半轴上,已知OB=2,∠AOB=30°.
如图,在平面直角坐标系中,Rt△OAB的斜边OB在x轴的正半轴上,点A在第一象限,将△OAB,使点O按逆时针方向旋转至△OA′B′,使点A的对应点A′落在y轴的正半轴上,已知OB=2,∠AOB=30°. 如图,边长为$\sqrt{3}$的等边△ABC中,D、E分别为AB、BC上的点,且DB=$\sqrt{2}$,将线段ED绕E点顺时针旋转60°得到线段EF,连CF.当∠FCB=30°时,CE的长为$\frac{1}{2}$($\sqrt{3}$+$\sqrt{2}$).
如图,边长为$\sqrt{3}$的等边△ABC中,D、E分别为AB、BC上的点,且DB=$\sqrt{2}$,将线段ED绕E点顺时针旋转60°得到线段EF,连CF.当∠FCB=30°时,CE的长为$\frac{1}{2}$($\sqrt{3}$+$\sqrt{2}$).
 如图,已知蚂蚁沿着长为2的正方体表面从点A出发,经过3个侧面爬到点B,如果它运动的路径是最短的,则此经过3个侧面的最短路径长为2$\sqrt{10}$.
如图,已知蚂蚁沿着长为2的正方体表面从点A出发,经过3个侧面爬到点B,如果它运动的路径是最短的,则此经过3个侧面的最短路径长为2$\sqrt{10}$.