题目内容
9.已知,抛物线y=(x-1)2-3(1)写出抛物线的开口方向是向上,顶点坐标是(1,-3),对称轴是x=1;
(2)直接写出当x取何值时函数y的最大或最小值为多少?
(3)当x<1时,函数y随x的增大而减小.
分析 (1)利用顶点式直接写出开口方向,对称轴,顶点坐标;
(2)根据开口方向与顶点坐标求得答案即可;
(3)利用函数的增减性得出答案即可.
解答 解:(1)写出抛物线的开口方向是向上,顶点坐标是(1,-3),对称轴是x=1;
(2)当x=1时,函数有最小值为-3;
(3)当x<1时,函数y随x的增大而减小.
故答案为:向上,(1,-3),x=1,<1.
点评 本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴直线x=-$\frac{b}{2a}$,以及抛物线的开口方向.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
19.下列正多边形的组合中,不能够铺满地面的是( )
| A. | 正八边形和正方形 | B. | 正五边形和正八边形 | ||
| C. | 正六边形和正三边形 |
20. 如图,EF是△ABC的中位线,若AE=4,AF=5,EF=6,则△AEF的周长是( )
如图,EF是△ABC的中位线,若AE=4,AF=5,EF=6,则△AEF的周长是( )
 如图,EF是△ABC的中位线,若AE=4,AF=5,EF=6,则△AEF的周长是( )
如图,EF是△ABC的中位线,若AE=4,AF=5,EF=6,则△AEF的周长是( )| A. | 7.5 | B. | 30 | C. | 15 | D. | 24 |
17.一元二次方程2x2+5x+2=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 不能确定 |
 如图,∠ABC=90°,∠C=15°,线段AC的垂直平分线DE交AC于D,交BC于E,D为垂足,CE=10cm,则AB=5 cm.
如图,∠ABC=90°,∠C=15°,线段AC的垂直平分线DE交AC于D,交BC于E,D为垂足,CE=10cm,则AB=5 cm.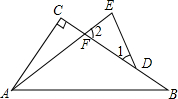 如图,在△ABC中,∠C=90°,F、D是BC上两点,E是AF延长线上一点,∠B=∠1,∠E=∠2,BF=kDE.试探究AB、BC、DE之间的数量关系.(用含有k的代数式表示)
如图,在△ABC中,∠C=90°,F、D是BC上两点,E是AF延长线上一点,∠B=∠1,∠E=∠2,BF=kDE.试探究AB、BC、DE之间的数量关系.(用含有k的代数式表示) 如图所示,用一根长为60cm的铁丝折成由两个小矩形组成的大矩形,设大矩形的一边长为x cm.
如图所示,用一根长为60cm的铁丝折成由两个小矩形组成的大矩形,设大矩形的一边长为x cm.