题目内容
13.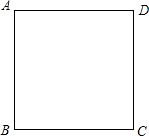 正方形、等边三角形是常见的轴对称图形.如图,设有一个边长为1的正方形ABCD,试在这个正方形中找出一个面积最大的和一个面积最小的内接等边三角形,并求出这两个图形的面积.
正方形、等边三角形是常见的轴对称图形.如图,设有一个边长为1的正方形ABCD,试在这个正方形中找出一个面积最大的和一个面积最小的内接等边三角形,并求出这两个图形的面积.
分析 ①如图1中,当点E是AB中点时,等边三角形△EFG的边长最小,在RT△AEF求出EF即可.②如图2中,当点G与点C重合,等边三角形△EFG的边长最长,在CD上取一点M使得EM=MC,根据对称性可知∠ECD=∠BCE=15°,设DF=x,列出方程即可解决问题.
解答 解:①如图1中,当点E是AB中点时,等边三角形△EFG的边长最小,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=1,AE=BE=$\frac{1}{2}$,∠A=∠B=90°,
∵∠FEG=60°,EF=EG,
在△AEF和△BEG中,
$\left\{\begin{array}{l}{EF=EG}\\{AE=BE}\end{array}\right.$,
∴△AEF≌△BEG,
∴∠AEF=∠BEG=60°,
∴EF=EG=FG=2AE=1.
S△EFG=$\frac{\sqrt{3}}{4}$•EF2=$\frac{\sqrt{3}}{4}$.
②如图2中,当点G与点C重合,等边三角形△EFG的边长最长.
在CD上取一点M使得EM=MC,根据对称性可知∠ECD=∠BCE=15°,
∴∠MFC=∠MCF=15°,
∴∠DMF=∠MFC+∠MCF=30°,设DF=a,则FM=MC=2a,DM=$\sqrt{3}$a,
∴2a+$\sqrt{3}$a=1,
∴a=2-$\sqrt{3}$,
∴DF=2-$\sqrt{3}$,CF2=CD2+DF2=8-4$\sqrt{3}$.
∴S△CEF=$\frac{\sqrt{3}}{4}$•CF2=2$\sqrt{3}$-3.
点评 本题考查正方形的性质、等边三角形的性质、勾股定理、全等三角形的判定和性质等知识,解题的关键是正确画出图形,添加辅助线构造特殊三角形解决问题,学会出现15°添加辅助线的方法,出现15°想到构造30°的直角三角形,属于中考常考题型.

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案| 每件的销售价x(元/件) | 200 | 190 | 180 | 170 | 160 | 150 | 140 |
| 每天的销售量y(件) | 80 | 90 | 100 | 110 | 120 | 130 | 140 |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,求第一周销售中,y与x的函数关系式;
(2)设第一周每天的赢利为w元,求w关于x的函数关系式,并求出每天的售价为多少元时,每天的赢利最大?最大赢利是多少?
(3)从第二周起,该店铺一直按第(2)中的最大日盈利的售价进行销售.但进入第三周后,网上其他购物店也陆续推出该型号童装,因此第三、四周该店铺每天的售价都比第二周下降了m%,销售量也比第二周下降了0.5m%(m<20);第五周开始,厂家给予该店铺优惠,每件的进价降低了16元;该店铺在维持第三、四周的销售价和销售量的基础上,同时决定每件童装的快递费由买家自付,这样,第五周的赢利相比第二周的赢利增加了2%,请估算整数m的值.
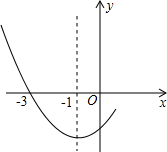 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0)下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(0,y2)是抛物线上的两点,则y1>y2.其中说法正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0)下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(0,y2)是抛物线上的两点,则y1>y2.其中说法正确的是( )| A. | ①② | B. | ②③ | C. | ①②④ | D. | ②③④ |
| A. | 5.433×107 | B. | 5.433×106 | C. | 543.3×104 | D. | 5433×103 |
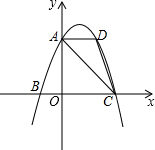 如图,已知二次函数y=ax2+bx+c(a≠0)的图象过A(0,3)、C(3,0)、D(2,3)三点.
如图,已知二次函数y=ax2+bx+c(a≠0)的图象过A(0,3)、C(3,0)、D(2,3)三点.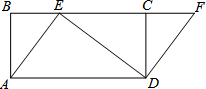 如图,四边形ABCD是矩形,点E在BC边上,点F在BC延长线上,且∠CDF=∠BAE.
如图,四边形ABCD是矩形,点E在BC边上,点F在BC延长线上,且∠CDF=∠BAE.