题目内容
19.直角三角形两直角边的和为6,则以此三角形的斜边为边长的正方形面积有( )| A. | 最大值18 | B. | 最大值26 | C. | 最小值18 | D. | 最小值26 |
分析 设一直角边长为x,表示出另一直角边,再利用勾股定理列式表示出斜边的平方,即为正方形的面积,然后整理出顶点式形式,再利用二次函数的最值问题求解.
解答 解:设一直角边长为x,则另一直角边(6-x),
由勾股定理得,斜边的平方=x2+(6-x)2=2x2-12x+36,
即正方形的面积=2x2-12x+36=2(x2-6x+9)+18=2(x-3)2+18,
所以,当x=3时,即三角形为等腰直角三角形时,以此三角形的斜边为边长的正方形面积有最小值为18.
故选C.
点评 本题考查了二次函数的最值问题,此类题目,整理出顶点式形式求解更简便.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.-32的相反数是( )
| A. | 6 | B. | -6 | C. | 9 | D. | -9 |
14.关于x的不等式(a-1)x-1>0的解集是x<b,则b与a的关系式为( )
| A. | b=$\frac{1}{a-1}$ | B. | b=-$\frac{1}{a-1}$ | C. | b=a-1 | D. | b=-a+1 |
8.下列事件中为必然事件的是( )
| A. | 打开电视机,正在播放湛江新闻 | B. | 下雨后,天空出现彩虹 | ||
| C. | 随机掷一枚硬币,落地后正面朝上 | D. | 早晨的太阳从东方升起 |
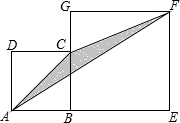 如图,四边形ABCD和四边形BEFG均为正方形,且A、B、E三点共线,正方形ABCD的边长为4,则S△ACF的面积为8.
如图,四边形ABCD和四边形BEFG均为正方形,且A、B、E三点共线,正方形ABCD的边长为4,则S△ACF的面积为8. 如图,点A,B和点C,D分别在两个同心圆上,且AD=BC,∠AOB与∠COD相等?请说明你的理由.
如图,点A,B和点C,D分别在两个同心圆上,且AD=BC,∠AOB与∠COD相等?请说明你的理由.