题目内容
4. 如图,点A,B和点C,D分别在两个同心圆上,且AD=BC,∠AOB与∠COD相等?请说明你的理由.
如图,点A,B和点C,D分别在两个同心圆上,且AD=BC,∠AOB与∠COD相等?请说明你的理由.
分析 运用“SSS”证明△COB≌DOA,则∠COB=∠DOA,根据等式性质得到∠AOB=∠COD.
解答 解:∠AOB=∠COD
证明:在△COB和△DOA中
$\left\{\begin{array}{l}{CO=DO}\\{AO=B0}\\{BC=AD}\end{array}\right.$,
∴△COB≌DOA,
∴∠COB=∠DOA,
∴∠AOC+∠AOB=∠AOC+∠COD,
∴∠AOB=∠COD.
点评 本题考查了全等三角形的判定与性质、同圆半径相等的性质,熟悉全等三角形的判定方法和圆的有关性质是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.直角三角形两直角边的和为6,则以此三角形的斜边为边长的正方形面积有( )
| A. | 最大值18 | B. | 最大值26 | C. | 最小值18 | D. | 最小值26 |
 如图,一个正方形和一个长方形重叠在一起,重叠部分是边长为3的正方形,求阴影部分的面积.
如图,一个正方形和一个长方形重叠在一起,重叠部分是边长为3的正方形,求阴影部分的面积. 如图所示,BD=CE,添加一个条件,使∠ABE=∠ACD(利用“SSS”判定),并给予证明.
如图所示,BD=CE,添加一个条件,使∠ABE=∠ACD(利用“SSS”判定),并给予证明.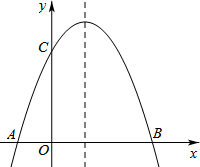 如图,已知抛物线y=ax2-2ax+3(a≠0)与x轴交于A、B两点,与y轴交于点C,且OB=3OA.
如图,已知抛物线y=ax2-2ax+3(a≠0)与x轴交于A、B两点,与y轴交于点C,且OB=3OA.